Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Williams, Kenneth S
1971.
A distribution property of the solutions of a congruence modulo a large prime.
Journal of Number Theory,
Vol. 3,
Issue. 1,
p.
19.


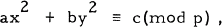
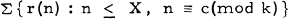 where r(n) denotes the number of representations of n as the sum of two squares.
where r(n) denotes the number of representations of n as the sum of two squares.