Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nakazi, Takahiko
2004.
Factorizations of functions in Hp (Tn ).
Complex Variables, Theory and Application: An International Journal,
Vol. 49,
Issue. 5,
p.
323.


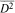 be the closed bidisc and
be the closed bidisc and 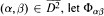 be a slice map, that is,
be a slice map, that is, 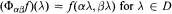 and
and 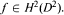 Then ker Φ
Then ker Φ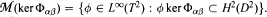 In this paper, we study the set
In this paper, we study the set 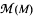 of all multipliers for an invariant subspace M such that the common zero set of
of all multipliers for an invariant subspace M such that the common zero set of 