Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T19:54:56.469Z Has data issue: false hasContentIssue false
  • English
  • Français

The Sizes of Rearrangements of Cantor Sets

Published online by Cambridge University Press:  20 November 2018

Kathryn E. Hare ,
Franklin Mendivil  and
Leandro Zuberman
Kathryn E. Hare
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON e-mail: [email protected]
Franklin Mendivil
Affiliation:
Department of Mathematics and Statistics, Acadia University, Wolfville, NS e-mail: [email protected]
Leandro Zuberman
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A linear Cantor set 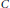$C$ with zero Lebesgue measure is associated with the countable collection of the bounded complementary open intervals. A rearrangment of 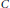$C$ has the same lengths of its complementary intervals, but with different locations. We study the Hausdorff and packing $h$-measures and dimensional properties of the set of all rearrangments of some given 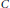$C$ for general dimension functions $h$. For each set of complementary lengths, we construct a Cantor set rearrangement which has the maximal Hausdorff and the minimal packing $h$-premeasure, up to a constant. We also show that if the packing measure of this Cantor set is positive, then there is a rearrangement which has infinite packing measure.

Keywords

28A7828A80Hausdorff dimensionpacking dimensiondimension functionsCantor setscut-out set
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 354 - 365
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Borel, É., Éléments de la Théorie des Ensembles. É ditions Albin Michel, Paris, 1949.Google Scholar
[2] Besicovitch, A. S. and Taylor, S. J.. On the complementary intervals of a linear closed set of zero Lebesgue measure. J. London Math. Soc. 29(1954), 449–459. http://dx.doi.org/10.1112/jlms/s1-29.4.449 Google Scholar
[3] Cabrelli, C., Hare, K., and Molter, U., Classifying Cantor sets by their fractal dimension. Proc. Amer. Math. Soc. 138(2010), no. 11, 3965–3974. http://dx.doi.org/10.1090/S0002-9939-2010-10396-9 Google Scholar
[4] Cabrelli, C., Mendivil, F., Molter, U., and Shonkwiler, R., On the h-Hausdorff measure of Cantor sets. Pacific J. Math. 217(2004), no. 1, 45–59. http://dx.doi.org/10.2140/pjm.2004.217.45 Google Scholar
[5] Falconer, K. J., Fractal Geometry: Mathematical Foundations and Applications. JohnWiley & Sons, Chichester, 1990.Google Scholar
[6] Falconer, K. J., Techniques in Fractal Geometry. JohnWiley & Sons, Chichester, 1997.Google Scholar
[7] Feng, D.-J., Exact packing measure of linear Cantor sets. Math. Nachr. 248/249(2003), 102–109. http://dx.doi.org/10.1002/mana.200310006Google Scholar
[8] Feng, D.-J., Hua, S., and Z.Wen, The pointwise densities of the Cantor measure. J. Math. Anal. Appl. 250(2000), no. 2, 692–705. http://dx.doi.org/10.1006/jmaa.2000.7137 Google Scholar
[9] Garcia, I., Molter, U., and Scotto, R., Dimension functions of Cantor sets. Proc. Amer. Math. Soc. 135(2007), no. 10, 3151–3161.(electronic). http://dx.doi.org/10.1090/S0002-9939-07-09019-3 Google Scholar
[10] He, C. Q. and Lapidus, M. L., Generalized Minkowski content, spectrum of fractal drums, fractal strings and the Riemann zeta-function. Mem. Amer. Math. Soc. 127(1997) no. 608.Google Scholar
[11] Joyce, H. and Preiss, D., On the existence of subsets of finite positive packing measure. Mathematika 42(1995), no. 1, 15–24. http://dx.doi.org/10.1112/S002557930001130X Google Scholar
[12] Larman, D. G., On Hausdorff measure in finite-dimensional compact metric spaces. Proc. London Math. Soc. 17(1967), 193–206. http://dx.doi.org/10.1112/plms/s3-17.2.193 Google Scholar
[13] Lapidus, L. and van Frankenhuijsen, M., Fractal Geometry, Complex Dimensions and Zeta Functions. Geometry and Spectra of Fractal Strings. Springer, New York, 2006.Google Scholar
[14] Peetre, J., Concave majorants of positive functions. Acta Math. Acad. Sci. Hungar. 21(1970), 327–333. http://dx.doi.org/10.1007/BF01894779 Google Scholar
[15] Rogers, C. A., Hausdorff Measures. Reprint of the 1970 original. Cambridge University Press, Cambridge, 1998.Google Scholar
[16] Taylor, J. and Tricot, C., Packing measure and its evaluation for a Brownian path. Trans. Amer. Math. Soc. 288(1985), no. 2, 679–699. http://dx.doi.org/10.1090/S0002-9947-1985-0776398-8 Google Scholar
[17] Tricot, C., Two definitions of fractional dimension. Math. Proc. Camb. Philos. Soc. 91(1982), no. 1, 57–74. http://dx.doi.org/10.1017/S0305004100059119 Google Scholar
[18] Wen, S. and Wen, Z., Some properties of packing measure with doubling gauge. Studia Math. 165(2004), no. 2, 125–134. http://dx.doi.org/10.4064/sm165-2-3 Google Scholar
[19] Xiong, Y. and Wu, M., Category and dimensions for cut-out sets. J. Math. Anal. Appl. 358(2009), no. 1, 125–135. http://dx.doi.org/10.1016/j.jmaa.2009.04.057 Google Scholar