Article contents
A Singular Critical Potential for the Schrödinger Operator
Published online by Cambridge University Press: 20 November 2018
Abstract
Consider a real potential 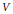 $V$ on
$V$ on 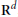 ${{\text{R}}^{d}}$,
${{\text{R}}^{d}}$, 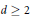 $d\ge 2$, and the Schrödinger equation:
$d\ge 2$, and the Schrödinger equation:
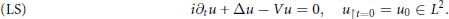 $$\left( \text{LS} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i{{\partial }_{t}}u+\Delta u-Vu=0,{{u}_{\upharpoonright }}_{t=0}={{u}_{0}}\in {{L}^{2}}$$
$$\left( \text{LS} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i{{\partial }_{t}}u+\Delta u-Vu=0,{{u}_{\upharpoonright }}_{t=0}={{u}_{0}}\in {{L}^{2}}$$
In this paper, we investigate the minimal local regularity of 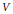 $V$ needed to get local in time dispersive estimates (such as local in time Strichartz estimates or local smoothing effect with gain of
$V$ needed to get local in time dispersive estimates (such as local in time Strichartz estimates or local smoothing effect with gain of 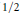 $1/2$ derivative) on solutions of
$1/2$ derivative) on solutions of 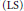 $\left( \text{LS} \right)$. Prior works show some dispersive properties when
$\left( \text{LS} \right)$. Prior works show some dispersive properties when 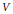 $V$ (small at infinity) is in
$V$ (small at infinity) is in
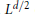 ${{L}^{d/2}}$ or in spaces just a little larger but with a smallness condition on
${{L}^{d/2}}$ or in spaces just a little larger but with a smallness condition on 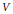 $V$ (or at least on its negative part).
$V$ (or at least on its negative part).
In this work, we prove the critical character of these results by constructing a positive potential 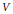 $V$ which has compact support, bounded outside 0 and of the order
$V$ which has compact support, bounded outside 0 and of the order 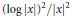 ${{\left( \log \left| x \right| \right)}^{2}}/{{\left| x \right|}^{2}}$ near 0. The lack of dispersiveness comes from the existence of a sequence of quasimodes for the operator
${{\left( \log \left| x \right| \right)}^{2}}/{{\left| x \right|}^{2}}$ near 0. The lack of dispersiveness comes from the existence of a sequence of quasimodes for the operator 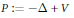 $P:=-\Delta +V$.
$P:=-\Delta +V$.
The elementary construction of 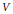 $V$ consists in sticking together concentrated, truncated potential wells near 0. This yields a potential oscillating with infinite speed and amplitude at 0, such that the operator
$V$ consists in sticking together concentrated, truncated potential wells near 0. This yields a potential oscillating with infinite speed and amplitude at 0, such that the operator 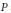 $P$ admits a sequence of quasi-modes of polynomial order whose support concentrates on the pole.
$P$ admits a sequence of quasi-modes of polynomial order whose support concentrates on the pole.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 10
- Cited by


