Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T06:46:55.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Simplicity of Partial Skew Group Rings of Abelian Groups

Published online by Cambridge University Press:  20 November 2018

Daniel Gonçalves
Daniel Gonçalves*
Affiliation:
Departamento de Matemática, Universidade Federal de Santa Catarina, Florianópolis, 88040-900, Brasil e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

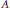Let $A$ be a ring with local units, 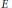$E$ a set of local units for 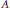$A$, 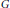$G$ an abelian group, and $\alpha$ a partial action of 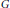$G$ by ideals of 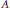$A$ that contain local units. We show that 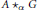$\text{A}\,{{\star }_{\alpha }}\,G$ is simple if and only if 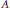$A$ is 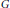$G$-simple and the center of the corner 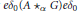$e{{\delta }_{0}}\left( \text{A}\,{{\star }_{\alpha }}\,G \right)e{{\delta }_{0}}$ is a field for all 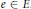$e\,\in \,E$. We apply the result to characterize simplicity of partial skew group rings in two cases, namely for partial skew group rings arising from partial actions by clopen subsets of a compact set and partial actions on the set level.

Keywords

16S3537B05partial skew group ringssimple ringspartial actionsabelian groups
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 511 - 519
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Ávila, J. and Ferrero, M., Closed and prime ideals in partial skew group rings of abelian groups. J. Algebra Appl. 10 (2011), no. 5, 961–978. http://dx.doi.org/10.1142/S0219498811005063 Google Scholar
[2] Beuter, V. and Gonçalves, D., Partial crossed products as equivalence relation algebras. RockyMountain J. Math., to appear.Google Scholar
[3] Boava, G. and Exel, R., Partial crossed product description of the C*-algebras associated with integral domains. Proc. Amer. Math. Soc. 141 (2013), no. 7, 2439–2451. http://dx.doi.org/10.1090/S0002-9939-2013-11724-7 Google Scholar
[4] Crow, K., Simple regular skew group rings. J. Algebra Appl. 4 (2005), no. 2, 127–137. http://dx.doi.org/10.1142/S0219498805000909 Google Scholar
[5] Dokuchaev, M. and Exel, R., Associativity of crossed products by partial actions, enveloping actions and partial representations. Trans. Amer. Math. Soc. 357 (2005), no. 5, 1931–1952. http://dx.doi.org/10.1090/S0002-9947-04-03519-6 Google Scholar
[6] Exel, R., Giordano, T., and Gonçalves, D., Envelope algebras of partial actions as groupoid C*-algebras. J. Operator Theory 65 (2011), no. 1, 197–210.Google Scholar
[7] Exel, R., Laca, M., and Quigg, J., Partial dynamical systems and C*-algebras generated by partial isometries. J. Operator Theory 47 (2002), no. 1, 169–186.Google Scholar
[8] Fisher, J.W. and Montgomery, S., Semiprime skew group rings. J. Algebra 52 (1978), no. 1, 241–247. http://dx.doi.org/10.1016/0021-8693(78)90272-7 Google Scholar
[9] Gonçalves, D. and Royer, D., Leavitt path algebras as partial skew group rings. Comm. Algebra 42 (2014), no. 8, 3578-3592. http://dx.doi.org/10.1080/00927872.2013.790038 Google Scholar
[10] Montgomery, S., Fixed rings of finite automorphism groups of associative rings. Lecture Notes in Mathematics, 818, Springer, Berlin, 1980.Google Scholar
[11] Öinert, J., Simplicity of skew group rings of abelian groups. Comm. Algebra 42 (2014), no. 2, 831–841.Google Scholar
[12] Passman, D. S., Infinite crossed products. Pure and Applied Mathematics, 135, Academic Press, Inc., Boston, MA, 1989.Google Scholar