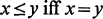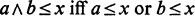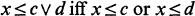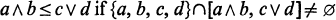Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jónsson, B.
1971.
Relatively free products of lattices.
Algebra Universalis,
Vol. 1,
Issue. 1,
p.
362.
Baker, Kirby A.
and
Hales, Alfred W.
1974.
From a lattice to its ideal lattice.
Algebra Universalis,
Vol. 4,
Issue. 1,
p.
250.
Day, Alan
1977.
Splitting lattices generate all lattices.
Algebra Universalis,
Vol. 7,
Issue. 1,
p.
163.
Davey, Brian A.
and
Sands, Bill
1977.
An application of Whitman's condition to lattices with no infinite chains.
Algebra Universalis,
Vol. 7,
Issue. 1,
p.
171.
Day, Alan
1977.
Contributions to Universal Algebra.
p.
57.
Sands, Bill
1977.
On a problem involving bounded epimorphisms of lattices.
Algebra Universalis,
Vol. 7,
Issue. 1,
p.
211.
1978.
General Lattice Theory.
Vol. 75,
Issue. ,
p.
316.
Day, Alan
1978.
Idempotents in The Groupoid of all SP Classes of Lattices.
Canadian Mathematical Bulletin,
Vol. 21,
Issue. 4,
p.
499.
García, O. C.
and
de la Peña, J. A.
1983.
Lattices with a finite Whitman cover.
algebra universalis,
Vol. 16,
Issue. 1,
p.
186.
Katriňák, Tibor
1984.
Splittingp-algebras.
Algebra Universalis,
Vol. 18,
Issue. 2,
p.
199.
Cz�dli, G�bor
and
Day, Alan
1984.
Horn sentences with (W) and weak Mal'cev conditions.
Algebra Universalis,
Vol. 19,
Issue. 2,
p.
217.
Freese, Ralph
and
Nation, J. B.
1985.
Covers in free lattices.
Transactions of the American Mathematical Society,
Vol. 288,
Issue. 1,
p.
1.
Lee, Jeh Gwon
1985.
Almost distributive lattice varieties.
Algebra Universalis,
Vol. 21,
Issue. 2-3,
p.
280.
Nation, J. B.
1985.
Universal Algebra and Lattice Theory.
Vol. 1149,
Issue. ,
p.
198.
Day, Alan
Nation, J. B.
and
Tschantz, Steve
1989.
Doubling convex sets in lattices and a generalized semidistributivity condition.
Order,
Vol. 6,
Issue. 2,
p.
175.
Gedeonov�, Eva
1990.
Constructions of S-lattices.
Order,
Vol. 7,
Issue. 3,
p.
249.
Freese, Ralph
Pickering, Douglas
and
Roddy, Michael
1991.
Obituary: A. Alan Day.
Order,
Vol. 8,
Issue. 4,
p.
319.
Geyer, Winfried
1993.
Generalizing semidistributivity.
Order,
Vol. 10,
Issue. 1,
p.
77.
Geyer, W.
1994.
The generalized doubling construction and formal concept analysis.
Algebra Universalis,
Vol. 32,
Issue. 3,
p.
341.
Day, Alan
1994.
Congruence normality: The characterization of the doubling class of convex sets.
Algebra Universalis,
Vol. 31,
Issue. 3,
p.
397.