Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-17T13:16:26.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple Helices on Fano Threefolds

Published online by Cambridge University Press:  20 November 2018

A. Polishchuk
A. Polishchuk*
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97405, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Building on the work of Nogin, we prove that the braid group 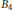${{B}_{4}}$ acts transitively on full exceptional collections of vector bundles on Fano threefolds with 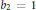${{b}_{2}}\,=\,1$ and 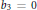${{b}_{3}}\,=\,0$. Equivalently, this group acts transitively on the set of simple helices (considered up to a shift in the derived category) on such a Fano threefold. We also prove that on threefolds with 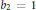${{b}_{2}}\,=\,1$ and very ample anticanonical class, every exceptional coherent sheaf is locally free.

Keywords

14F0514J45
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 3 , 01 September 2011 , pp. 520 - 526
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Beilinson, A. A., Coherent sheaves on ℙ n and problems in linear algebra. (Russian) Funktsional Anal. i Prilozhen. 12(1978), no. 3, 68–69.Google Scholar
[2] Bogomolov, F. A., Stable vector bundles on projective surfaces. (Russian) Mat. Sb. 185(1994), no. 4, 3–26; translation in Russian Acad. Sci. Sb. Math. 81(1995), no. 2, 397–419.Google Scholar
[3] Bondal, A. I., Representations of associative algebras and coherent sheaves. Math. USSR-Izv. 34(1990), no. 1, 23–42.Google Scholar
[4] Bondal, A. I. and Polishchuk, A. E., Homological properties of associative algebras: the method of helices. Russian Acad. Sci. Izv. Math. 42(1994), no. 2, 219–260.Google Scholar
[5] Bridgeland, T., t-structures on some local Calabi-Yau varieties. J. Algebra 289(2005), no. 2, 453–483. doi:10.1016/j.jalgebra.2005.03.016Google Scholar
[6] Crawley-Boevey, W., Exceptional sequences of representations of quivers. In: Representations of algebras (Ottawa, ON, 1992), CMS Conf. Proc., American Mathematical Society, Providence, RI, 1993, pp. 117–124.Google Scholar
[7] Gorodentsev, A. L. and Kuleshov, S. A., Helix theory. Mosc. Math. J. 4(2004), no. 2, 377–440, 535.Google Scholar
[8] Iskovskikh, V. A. and Prokhorov, Yu. G., Fano varieties. Algebraic geometry, V, Encyclopaedia Math. Sci., 47, Springer, Berlin, 1999, pp. 1–247.Google Scholar
[9] Ishii, A. and Uehara, H., Autoequivalences of derived categories on the minimal resolutions of An-singularities on surfaces. J. Differential Geom. 71(2005), no. 3, 385–435.Google Scholar
[10] Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves. Friedr. Vieweg & Sohn, Braunschweig, 1997.Google Scholar
[11] Kapranov, M. M., Derived category of coherent bundles on a quadric. (Russian) Funktsional Anal. i Prilozhen. 20(1986), no. 2, 67.Google Scholar
[12] Kuleshov, S. A., Exceptional bundles on K3 surfaces. In: Helices and vector bundles, London Math. Soc. Lecture Note Ser., Cambridge University Press, Cambridge, 1990, pp. 105–114.Google Scholar
[13] Kuznetsov, A. G., An exceptional set of vector bundles on the varieties V 22 . Moscow Univ. Math. Bull. 51(1996), no. 3, 35–37.Google Scholar
[14] Langer, A., Lectures on torsion-free sheaves and their moduli. In: Algebraic cycles, sheaves, shtukas, and moduli, Trends Math., Birkhäuser, Basel, 2008, pp. 69–103.Google Scholar
[15] Miró-Roig, R. M. and Soares, H., The stability of exceptional bundles on complete intersection 3-folds. Proc. Amer. Math. Soc. 136(2008), no. 11, 3751–3757. doi:10.1090/S0002-9939-08-09258-7Google Scholar
[16] Moĭsezon, B., Algebraic homology classes on algebraic varieties. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 31(1967), 225–268.Google Scholar
[17] Mukai, S., On the moduli space of bundles on K3 surfaces. I. In: Vector bundles on algebraic varieties (Bombay, 1984), Tata Inst. Fund. Res., Bombay, 1987, pp. 341–413.Google Scholar
[18] Mumford, D., Lectures on curves on an algebraic surface. Annals of Mathematics Studies, 59, Princeton University Press, Princeton, NJ, 1966.Google Scholar
[19] Nogin, D. Yu., Helices on some Fano threefolds: constructivity of semiorthogonal bases of K 0 . Ann. Sci. é cole Norm. Sup. (4) 27(1994), no. 2, 129–172.Google Scholar
[20] Orlov, D. O., Exceptional set of vector bundles on the variety V 5 . Moscow Univ. Math. Bull. 46(1991), no. 5, 48–50.Google Scholar
[21] Positselski, L., All strictly exceptional collections in consist of vector bundles. arXiv:alg-geom/9507014v1.Google Scholar
[22] Seidel, P. and Thomas, R., Braid group actions on derived categories of coherent sheaves. Duke Math. J. 108(2001), no. 1, 37–108. doi:10.1215/S0012-7094-01-10812-0Google Scholar
[23] Zube, D. Yu., The stability of exceptional bundles on three-dimensional projective space. In: Helices and vector bundles, London Math. Soc. Lecture Note Ser., 148, Cambridge University Press, Cambridge, 1990, pp. 115–117.Google Scholar