Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T18:21:04.475Z Has data issue: false hasContentIssue false
  • English
  • Français

The Shrinking Property

Published online by Cambridge University Press:  20 November 2018

Mary Ellen Rudin
Mary Ellen Rudin*
Affiliation:
University of Wisconsin Madison, Wisconsin 53706
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

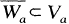A space has the shrinking property if, for every open cover {Va | a ∈ A}, there is an open cover {Wa | a ∈ A} with for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.

Keywords

54D2054D18shrinkingnormalparacompactDowker
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 4 , 01 December 1983 , pp. 385 - 388
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Dowker, C. H., On countably paracompact spaces, Can. J. Math. 3 (1971) 214-224.Google Scholar
2. Rudin, M. E., A normal space X for which X×I is not normal, Fund. Math. LXXIII (1971) 179-186.Google Scholar
3. Rudin, M. E., K-Dowker spaces, Czech. Math. J. 28 (1978) Praha, 324-326.Google Scholar
4. Gul'ko, S. P., On properties of subsets of ∑-products, Soviet Math. Dokl. 18 (1977), 1438-1442.Google Scholar
5. LeDonne, A., Normality and shrinking property in ∑-product of spaces, this Journal, to appear.Google Scholar