Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T07:27:26.243Z Has data issue: false hasContentIssue false
  • English
  • Français

A Sharp Constant for the Bergman Projection

Published online by Cambridge University Press:  20 November 2018

Marijan Marković
Marijan Marković*
Affiliation:
Faculty of Natural Sciences and Mathematics, University of Montenegro, Cetinjski put b.b., 81000 Podgorica, Montenegro. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the Bergman projection operator $P$ we prove that

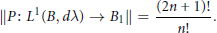$$\left\| P:\,{{L}^{1}}\left( B,\,d\lambda \right)\,\to \,{{B}_{1}} \right\|\,=\,\frac{\left( 2n\,+\,1 \right)!}{n!}.$$

Here $\lambda$ stands for the hyperbolic metric in the unit ball $B$ of 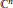${{\mathbb{C}}^{n}}$, and 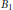${{B}_{1}}$ denotes the Besov space with an adequate semi-norm. We also consider a generalization of this result. This generalizes some recent results due to Perälä.

Keywords

45P0547B35Bergman projectionsBesov spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 128 - 133
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Andrews, G. E., R. Askey, and R. Roy, Special functions. Encyclopedia of Mathematics and its Applications, 71, Cambridge University Press, Cambridge, 1999.Google Scholar
[2] Kalaj, D. and Marković, M., Norm of the Bergman projection. Math. Scand., to appear.Google Scholar
[3] Kalaj, D. and Vujadinović, Dj., Norm of the Bergman projection onto the Bloch space. J. Operator Theory, to appear.Google Scholar
[4] Marković, M., Semi-norms of the Bergman projection. arxiv:1402.4688Google Scholar
[5] Perälä, A., Sharp constant for the Bergman projection onto the minimal Möbius invariant space. Arch. Math. (Basel) 102 (2014), no. 3, 263–270. http://dx.doi.org/10.1007/s00013-014-0624-6 Google Scholar
[6] Rudin, W., Function theory in the unit ball of Cn. Grundlehren der MathematischenWissenschaften, 241, Springer-Verlag, New York-Berlin, 1980.Google Scholar
[7] Zhu, K., Spaces of holomorphic functions in the unit ball. Graduate Texts in Mathematics, 226, Springer-Verlag, New York, 2005.Google Scholar