Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T09:26:46.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Separable Quotients of Free Topological Groups

Part of: Fairly general properties Maps and general types of spaces defined by maps Topological and differentiable algebraic systems

Published online by Cambridge University Press:  29 November 2019

Arkady Leiderman  and
Mikhail Tkachenko
Arkady Leiderman
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beer Sheva, P.O.B. 653, Israel Email: [email protected]
Mikhail Tkachenko
Affiliation:
Departamento de Matemáticas, Universidad Autónoma Metropolitana, Av. San Rafael Atlixco 186, Col. Vicentina, Del. Iztapalapa, C.P. 09340, Mexico City, Mexico Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the following problem: For which Tychonoff spaces 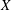$X$ do the free topological group 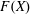$F(X)$ and the free abelian topological group 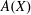$A(X)$ admit a quotient homomorphism onto a separable and nontrivial (i.e., not finitely generated) group? The existence of the required quotient homomorphisms is established for several important classes of spaces 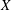$X$, which include the class of pseudocompact spaces, the class of locally compact spaces, the class of $\unicode[STIX]{x1D70E}$-compact spaces, the class of connected locally connected spaces, and some others.

We also show that there exists an infinite separable precompact topological abelian group 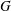$G$ such that every quotient of 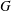$G$ is either the one-point group or contains a dense non-separable subgroup and, hence, does not have a countable network.

Keywords

free topological groupquotientseparable

MSC classification

Primary: 22A05: Structure of general topological groups
Secondary: 54D65: Separability 54C10: Special maps on topological spaces (open, closed, perfect, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 610 - 623
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author M. T. gratefully acknowledges the financial support received from the Center for Advanced Studies in Mathematics of the Ben Gurion University of the Negev during his visit in May, 2019.

References

Arhangel’skii, A. V. and Tkachenko, M. G., Topological groups and related structures. Atlantis Studies in Mathematics, 1, Atlantis Press, Paris; World Scientific, Hackensack, NJ, 2008. https://doi.org/10.2991/978-94-91216-35-0CrossRefGoogle Scholar
Banakh, T., Ka̧kol, J., and Śliwa, W., Metrizable quotients of C p-spaces. Topol. Appl. 249(2018), 95–102. https://doi.org/10.1016/j.topol.2018.09.012CrossRefGoogle Scholar
Graev, M. I., Free topological groups. (Russian). Izvestiya Akad. Nauk SSSR Ser. Mat. 12(1948), 279–324. English translation in: Topology and Topological Algebra Translations Series 1, vol. 8 (1962), American Mathematical Society, pp. 305–364.Google Scholar
Karnik, S. M. and Willard, S., Natural covers and r-quotient mappings. Canad. Math. Bull. 25(1982), 456–461. https://doi.org/10.4153/CMB-1982-065-1CrossRefGoogle Scholar
Ka̧kol, J. and Śliwa, W., Efimov spaces and the separable quotient problem for spaces C p(X). J. Math. Anal. Appl. 457(2018), 104–113. https://doi.org/10.1016/j.jmaa.2017.08.010CrossRefGoogle Scholar
Leiderman, A. G. and Morris, S. A., Separability of topological groups: a survey with open problems. Axioms 8(2019), 1–18. https://doi.org/10.3390/axioms8010003Google Scholar
Leiderman, A. G., Morris, S. A., and Tkachenko, M. G., The separable quotient problem for topological groups. Israel J. Math. 234(2019), no. 1, 331–369. https://doi.org/10.1007/s11856-019-1931-1CrossRefGoogle Scholar
Markov, A. A., On free topological groups. In: Topology and topological algebra, Translation Series 1, vol. 8, American Math. Society, Providence, RI, 1962, pp. 195–272. Russian original in: Izv. Akad. Nauk SSSR 9(1945), 3–64.Google Scholar
Morris, S. A. and Nickolas, P., Locally compact group topologies on algebraic free product of groups. J. Algebra 38(1976), 393–397. https://doi.org/10.1016/0021-8693(76)90229-5CrossRefGoogle Scholar
Okunev, O. G., A method for constructing examples of M-equivalent spaces. Topol. Appl. 36(1990), 157–171; correction: Topol. Appl. 49(1993), 191–192. https://doi.org/10.1016/0166-8641(93)90044-ECrossRefGoogle Scholar
Okunev, O. and Tamano, K., Lindelöf powers and products of function spaces. Proc. Amer. Math. Soc. 124(1996), 2905–2916. https://doi.org/10.1090/S0002-9939-96-03629-5CrossRefGoogle Scholar
Sánchez, I. and Tkachenko, M., Products of bounded subsets of paratopological groups. Topol. Appl. 190(2015), 42–58. https://doi.org/10.1016/j.topol.2015.03.017CrossRefGoogle Scholar