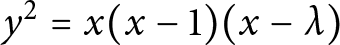Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dokchitser, Vladimir
and
Morgan, Adam
2023.
A note on hyperelliptic curves with ordinary reduction over 2-adic fields.
Journal of Number Theory,
Vol. 244,
Issue. ,
p.
264.