Article contents
Second-order Riesz Transforms and Maximal Inequalities Associated with Magnetic Schr ödinger Operators
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 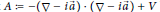 $A\,:=\,-\,\left( \nabla \,-\,i\overrightarrow{a} \right)\,.\,\left( \nabla \,-\,i\overrightarrow{a} \right)\,+\,V$ be a magnetic Schrödinger operator on
$A\,:=\,-\,\left( \nabla \,-\,i\overrightarrow{a} \right)\,.\,\left( \nabla \,-\,i\overrightarrow{a} \right)\,+\,V$ be a magnetic Schrödinger operator on 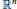 ${{\mathbb{R}}^{n}}$, where
${{\mathbb{R}}^{n}}$, where
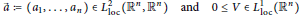 $$\vec{a}:=\left( {{a}_{1}},...,{{a}_{n}} \right)\in L_{\text{loc}}^{2}\left( {{\mathbb{R}}^{n}},{{\mathbb{R}}^{n}} \right)\operatorname{and}0\le V\in L_{\text{loc}}^{1}\left( {{\mathbb{R}}^{n}} \right)$$
$$\vec{a}:=\left( {{a}_{1}},...,{{a}_{n}} \right)\in L_{\text{loc}}^{2}\left( {{\mathbb{R}}^{n}},{{\mathbb{R}}^{n}} \right)\operatorname{and}0\le V\in L_{\text{loc}}^{1}\left( {{\mathbb{R}}^{n}} \right)$$
satisfy some reverse Hölder conditions. Let 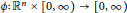 $\phi :\,{{\mathbb{R}}^{n}}\,\times \,[0,\,\infty )\,\to \,[0,\,\infty )$ be such that
$\phi :\,{{\mathbb{R}}^{n}}\,\times \,[0,\,\infty )\,\to \,[0,\,\infty )$ be such that 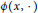 $\phi \left( x,\,. \right)$ for any given
$\phi \left( x,\,. \right)$ for any given 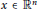 $x\,\in \,{{\mathbb{R}}^{n}}$ is an Orlicz function,
$x\,\in \,{{\mathbb{R}}^{n}}$ is an Orlicz function, 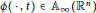 $\phi \left( ^{.}\,,\,t \right)\,\in \,{{\mathbb{A}}_{\infty }}\left( {{\mathbb{R}}^{n}} \right)$ for all
$\phi \left( ^{.}\,,\,t \right)\,\in \,{{\mathbb{A}}_{\infty }}\left( {{\mathbb{R}}^{n}} \right)$ for all 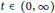 $t\,\in \,\left( 0,\,\infty \right)$ (the class of uniformly Muckenhoupt weights) and its uniformly critical upper type index
$t\,\in \,\left( 0,\,\infty \right)$ (the class of uniformly Muckenhoupt weights) and its uniformly critical upper type index 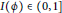 $I\left( \phi \right)\,\in \,(0,\,1]$. In this article, the authors prove that second-order Riesz transforms
$I\left( \phi \right)\,\in \,(0,\,1]$. In this article, the authors prove that second-order Riesz transforms 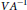 $V{{A}^{-1}}$ and
$V{{A}^{-1}}$ and 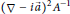 ${{\left( \nabla \,-\,i\overrightarrow{a} \right)}^{2}}{{A}^{-1}}$ are bounded from the Musielak–Orlicz–Hardy space
${{\left( \nabla \,-\,i\overrightarrow{a} \right)}^{2}}{{A}^{-1}}$ are bounded from the Musielak–Orlicz–Hardy space 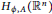 ${{H}_{\phi ,\,A}}\left( {{\mathbb{R}}^{n}} \right)$, associated with
${{H}_{\phi ,\,A}}\left( {{\mathbb{R}}^{n}} \right)$, associated with 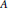 $A$, to theMusielak–Orlicz space
$A$, to theMusielak–Orlicz space 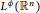 ${{L}^{\phi }}\left( {{\mathbb{R}}^{n}} \right)$. Moreover, we establish the boundedness of
${{L}^{\phi }}\left( {{\mathbb{R}}^{n}} \right)$. Moreover, we establish the boundedness of 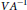 $V{{A}^{-1}}$ on
$V{{A}^{-1}}$ on 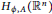 ${{H}_{\phi ,\,A}}\left( {{\mathbb{R}}^{n}} \right)$. As applications, some maximal inequalities associated with
${{H}_{\phi ,\,A}}\left( {{\mathbb{R}}^{n}} \right)$. As applications, some maximal inequalities associated with 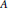 $A$ in the scale of
$A$ in the scale of 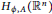 ${{H}_{\phi ,\,A}}\left( {{\mathbb{R}}^{n}} \right)$ are obtained.
${{H}_{\phi ,\,A}}\left( {{\mathbb{R}}^{n}} \right)$ are obtained.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 9
- Cited by


