Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T17:22:57.763Z Has data issue: false hasContentIssue false
  • English
  • Français

Second Variation of the "Total Scalar Curvature" on Contact Manifolds

Published online by Cambridge University Press:  20 November 2018

D. E. Blair  and
D. Perrone
D. E. Blair
Affiliation:
Department of Mathematics, Michigan State University East Lansing, Michigan 48824 U.S.A.
D. Perrone
Affiliation:
Dipartimento di Matematica, Eacoltá di Scienze, Universitá Degli Studi di Lecce, Via Arnesano, 73100 Lecce, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M2n+1 be a compact contact manifold and 𝓐 the set of associated metrics. Using the scalar curvature R and the *-scalar curvature R*, in [5] we defined the "total scalar curvature", by 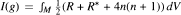and showed that the critical points of I(g) on 𝓐 are the K-contact metrics, i.e. metrics for which the characteristic vector field is Killing. In this paper we compute the second variation of I(g) and prove that the index of I(g) and of —I(g) are both positive at each critical point. As an application we show that the classical total scalar curvature A(g) = ∫M R dVg restricted to 𝓐 cannot have a local minimum at any Sasakian metric.

Keywords

58E1153C1553C25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 38 , Issue 1 , 01 March 1995 , pp. 16 - 22
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Blair, D. E., Contact Manifolds in Riemannian Geometry, Lecture Notes in Math. 509, Springer, Berlin, 1976.Google Scholar
2. Blair, D. E., On the set of metrics associated to a symplectic or contact form, Bull. Inst. Math. Acad. Sinica 11(1983), 297–308.Google Scholar
3. Blair, D. E., The “total scalar curvature“as a symplectic invariant, Proc. 3rd Congress of Geometry, Thessaloniki, 1991,79-83.Google Scholar
4. Blair, D. E. and Ledger, A. J., Critical associated metrics on contact manifolds II, J. Austral. Math. Soc. Ser. A 41(1986), 404–410.Google Scholar
5. Blair, D. E. and D. Perrone, A variational characterization of contact metric manifolds with vanishing torsion, Canad. Math. Bull., 35(1992), 455–462.Google Scholar
6. Chern, S. S. and Hamilton, R. S., On Riemannian metrics adapted to three-dimensional contact manifolds, Lecture Notes in Math. 1111, Springer, Berlin, 1985, 279–308.Google Scholar
7. Muto, Y., On Einstein metrics, J. Differential Geom. 9(1974), 521–530.Google Scholar
8. Olszak, Z, On contact metric manifolds, Tôhoku Math. J. 31(1979), 247–253.Google Scholar
9. Perrone, D., Torsion and critical metrics on contact three-manifolds, Kodai Math. J. 13(1990), 88–100.Google Scholar
10. Perrone, D., Torsion tensor and critical metrics on contact (2n+ \)-manifolds, Mh. Math. 114(1992), 245–259.Google Scholar