Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Philos, Ch. G.
1985.
Integral Averages and Second Order Superlinear Oscillation.
Mathematische Nachrichten,
Vol. 120,
Issue. 1,
p.
127.
Philos, Ch. G.
1986.
Integral averaging techniques for the oscillation of second order sublinear ordinarry differential equations.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 40,
Issue. 1,
p.
111.
Blaśko, Rudolf
Graef, John R
Haĉik, Miloš
and
Spikes, Paul W
1990.
Oscillatory behavior of solutions of nonlinear differential equations of the second order.
Journal of Mathematical Analysis and Applications,
Vol. 151,
Issue. 2,
p.
330.
Philos, Ch. G.
1990.
On Oscillation of Second Order Sublinear Ordinary Differential Equations with Alternating Coefficients.
Mathematische Nachrichten,
Vol. 146,
Issue. 7-12,
p.
105.
Philos, Ch.G
1990.
An oscillation criterion for superlinear differential equations of second order.
Journal of Mathematical Analysis and Applications,
Vol. 148,
Issue. 2,
p.
306.
Grace, S.R.
and
Lalli, B.S.
1990.
Integral averaging techniques for the oscillation of second order nonlinear differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 1,
p.
277.
Grace, S.R
and
Lalli, B.S
1990.
Asymptotic and oscillatory behavior of solutions of a class of second order differential equations with deviating arguments.
Journal of Mathematical Analysis and Applications,
Vol. 145,
Issue. 1,
p.
112.
Lalli, B.S.
and
Grace, S.R.
1990.
Asymptotic and oscillatory behavior of a class of second order functional differential equations.
Rocky Mountain Journal of Mathematics,
Vol. 20,
Issue. 4,
Grace, S. R.
and
Lalli, B. S.
1992.
Oscillation theorems for second order superlinear differential equations with damping.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 53,
Issue. 2,
p.
156.
Philos, C. G.
and
Purnaras, I. K.
1992.
On the oscillation of second order nonlinear differential equations.
Archiv der Mathematik,
Vol. 59,
Issue. 3,
p.
260.
Philos, Ch.G
and
Purnaras, I.K
1992.
Oscillations in superlinear differential equations of second order.
Journal of Mathematical Analysis and Applications,
Vol. 165,
Issue. 1,
p.
1.
Manojlović, J.V.
2001.
Integral averages and oscillation of second-order nonlinear differential equations.
Computers & Mathematics with Applications,
Vol. 41,
Issue. 12,
p.
1521.
Agarwal, Ravi P.
Grace, Said R.
and
O’Regan, Donal
2002.
Oscillation Theory for Second Order Linear, Half-Linear, Superlinear and Sublinear Dynamic Equations.
p.
273.
Agarwal, R.P
Grace, S.R
and
O'Regan, D
2004.
Linearization of second-order superlinear oscillation theorems.
Mathematical and Computer Modelling,
Vol. 39,
Issue. 9-10,
p.
1165.
Tiryaki, A.
and
Çakmak, D.
2004.
Integral averages and oscillation criteria of second-order nonlinear differential equations.
Computers & Mathematics with Applications,
Vol. 47,
Issue. 10-11,
p.
1495.
Li, Hui
Zhao, Yige
and
Han, Zhenlai
2019.
New oscillation criterion for Emden–Fowler type nonlinear neutral delay differential equations.
Journal of Applied Mathematics and Computing,
Vol. 60,
Issue. 1-2,
p.
191.


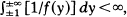 and
and 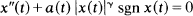 (γ > 1) this criterion leads to an oscillation result due to Wong [9].
(γ > 1) this criterion leads to an oscillation result due to Wong [9].