Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T10:39:47.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Second Order Operators with Non-Zero Eta Invariant

Published online by Cambridge University Press:  20 November 2018

H. D. Fegan
H. D. Fegan*
Affiliation:
Department of Mathematics and Statistics University of New Mexico Albuquerque, NM 87131 U. S. A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give an example of an elliptic second order pseudodifferential operator with a non-zero eta invariant. The operator is constructed on homogeneous bundles over compact Lie groups and is formed by composing differential operators and an operator of class 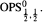In general it is not elliptic but in the special case of even dimensional bundles over SU(2) it is elliptic. The eta invariant is calculated in the special case and in the non elliptic case a difference eta invariant is obtained.

Keywords

58G15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 341 - 353
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Atiyah, M. F., Patodi, V. K. and Singer, I. M., Spectral Asymmetry and Riemannian Geometry I, II and III, Math Proc. Camb. Phil. Soc. 77(1975), 43–69; 78(1976), 405–432; and 79(1976), 71–99.Google Scholar
2. Bourbaki, N., Groupes etAlgebres de Lie, Ch. 4, 5 et 6 , Hermann, Paris, 1968.Google Scholar
3. Boutet, L. de Monvel and J. Sjôstrand, Sur la singulariete des noyaux de Bergman et de Szegô, Astérisque 34-36(1976), 123–164.Google Scholar
4. Fegan, H. D., Special Function Potentials for the Laplacian, Can. J. Math. 34(1982), 1183–1194.Google Scholar
5. Gilkey, Peter B., The Residue of the Local Eta Function at the Origin, Math. Ann. 240(1979), 183–189.Google Scholar
6. Gilkey, Peter B., The Residue of the Global Eta Function at the Origin, Adv. Math. 40(1981), 290–307.Google Scholar
7. Gilkey, Peter B., Invariance theory, the heat equation and the Atiyah-Singer index theorem , Publish or Perish Inc., 1984.Google Scholar
8. Gilkey, Peter B., The Eta Invariant of Even Order Operators , In: Differential Geometry, editors, Carreras, F. J., O. Medrano and Naviera, A. M., Lecture notes in Math 1410, Springer Verlag, Berlin, 1989.Google Scholar
9. Guillemin, V. and Uribe, A., Spectral Properties of a Certain Class of Complex Potentials, Trans. Amer. Math. Soc. 279(1983), 759–771.Google Scholar
10. Shanahan, Patrick, The Atiyah-Singer Index Theorem , Lecture notes in Math 638, Springer Verlag, Berlin, 1978.Google Scholar
11. Stolz, Stephan, Exotic Structures on 4 Manifolds Detected by Spectral Invariants, Invent. Math. 94(1988), 147–162.Google Scholar
12. Taylor, Michael E., Noncommutative Microlocal Analysis Part, I , Mem. of Amer. Math. Soc. 52(1984), number 313.Google Scholar
13. Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis , Cambridge Univ. Press, Cambridge, 1920.Google Scholar
14. Wodzicki, Mariusz, Spectral Asymmetry andZeta Functions, Invent. Math. 66(1982), 115–135. 15 , Local Invariants of Spectral Asymmetry, Invent. Math. 75(1984), 143–178.Google Scholar