Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T11:35:58.739Z Has data issue: false hasContentIssue false
  • English
  • Français

A Second Note on Ingham's Summation Method

Published online by Cambridge University Press:  20 November 2018

S. L. Segal
S. L. Segal*
Affiliation:
Department of Mathematics, The University of Rochester Rochester, New York 14627
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A series ∑ an is said to be summable (I) to the limit A if

(*)

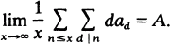
Clearly the limit is the same whether x→∞ through all real values or only positive integer values, and the expression whose limit is being taken can also be expressed in the two equivalent forms

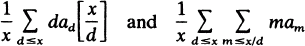
where [x] is the greatest integer ≤x.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 22 , Issue 1 , 01 March 1979 , pp. 117 - 120
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Erdös, P. and Segal, S. L., A note on Ingham's Summation Method, Jour. Number Theory, 10, (1978), 95-98.Google Scholar
2. Hardy, G. H. Divergent Series, Oxford, 1949.Google Scholar
3. Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, Oxford (4th edition, 1965).Google Scholar
4. Ingham, A. E., Some Tauberian Theorems connected with the Prime Number Theorem, J. London Math. Soc. 20, (1945), 171-180.Google Scholar
5. Rubel, L. A., An Abelian Theorem for Number-Theoretic Sums, Acta Arithmetica 6, (1960), 175-177, Correction Acta Arithmetica 6, (1961), 523.Google Scholar
6. Segal, S. L., Ingham's Summation Method and the Riemann Hypothesis, Proc. Lond. Math. Soc. (3) 30, (1975), 129-142, Carrijendum 34 (1977), 438.Google Scholar
7. Segal, S. L., On Ingham's Summation Method, Canadian Journal Math., 18, (1966), 97-105.Google Scholar
8. Wintner, A., Eratosthenian Averages, Baltimore, 1943.Google Scholar