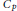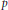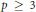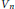Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sezer, Müfit
2011.
Explicit separating invariants for cyclic P-groups.
Journal of Combinatorial Theory, Series A,
Vol. 118,
Issue. 2,
p.
681.
PATTANAYAK, S. K.
2014.
ON SOME STANDARD GRADED ALGEBRAS IN MODULAR INVARIANT THEORY.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 01,
p.
1350080.
Derksen, Harm
and
Kemper, Gregor
2015.
Computational Invariant Theory.
p.
71.