Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T11:40:27.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Root Extensions and Factorization in Affine Domains

Published online by Cambridge University Press:  20 November 2018

P. Etingof ,
P. Malcolmson  and
F. Okoh
P. Etingof
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA e-mail: [email protected]
P. Malcolmson
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI 48202, USA e-mail: [email protected] e-mail: [email protected]
F. Okoh
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI 48202, USA e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integral domain $R$ is IDPF (Irreducible Divisors of Powers Finite) if, for every non-zero element $a$ in $R$, the ascending chain of non-associate irreducible divisors in $R$ of 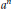${{a}^{n}}$ stabilizes on a finite set as $n$ ranges over the positive integers, while $R$ is atomic if every non-zero element that is not a unit is a product of a finite number of irreducible elements (atoms). A ring extension 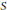$S$ of $R$ is a root extension or radical extension if for each $s$ in 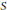$S$, there exists a natural number 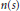$n\left( s \right)$ with 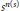${{s}^{n\left( s \right)}}$ in $R$. In this paper it is shown that the ascent and descent of the IDPF property and atomicity for the pair of integral domains 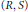$\left( R,\,S \right)$ is governed by the relative sizes of the unit groups 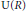$\text{U}\left( R \right)$ and 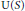$\text{U}\left( S \right)$ and whether 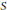$S$ is a root extension of $R$. The following results are deduced from these considerations: An atomic IDPF domain containing a field of characteristic zero is completely integrally closed. An affine domain over a field of characteristic zero is IDPF if and only if it is completely integrally closed. Let $R$ be a Noetherian domain with integral closure 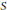$S$. Suppose the conductor of 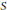$S$ into $R$ is non-zero. Then $R$ is IDPF if and only if 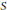$S$ is a root extension of $R$ and 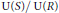$\text{U}\left( S \right)/\text{U}\left( R \right)$ is finite.

Keywords

13F1514A25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 247 - 255
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Anderson, D. D., Anderson, D. F., and Zafrullah, M., Factorization in integral domains. J. Pure Appl. Algebra 69(1990), no. 1, 1–19. doi:10.1016/0022-4049(90)90074-RGoogle Scholar
[2] Anderson, D. D. and Mullins, B., Finite factorization domains. Proc. Amer. Math. Soc. 124(1996), no. 2, 389–396. doi:10.1090/S0002-9939-96-03284-4Google Scholar
[3] Bourbaki, N., Commutative Algebra. Elements of Mathemetics, Springer-Verlag, Berlin, 1989.Google Scholar
[4] Brandis, A., Über die multiplikative Struktur von Körpererwiterungen. Math. Z. 87(1965), 71–73. doi:10.1007/BF01109932Google Scholar
[5] Chacron, M., Lawrence, J., and Madison, D., A note on radical extensions of rings. Canad. Math. Bull. 18(1975), no. 3, 423–424.Google Scholar
[6] Cohn, P. M., Bezout rings and their subrings. Proc. Cambridge Philos. Soc. 64(1968), 251–264. doi:10.1017/S0305004100042791Google Scholar
[7] Eakin, P. M., A note on finite-dimensional subrings of polynomial rings. Proc. Amer. Math. Soc 31(1972), 75–80. doi:10.2307/2038515Google Scholar
[8] Faith, C., Radical extensions of rings. Proc. Amer. Math. Soc. 12(1961), 274–283. doi:10.2307/2034321Google Scholar
[9] Geroldinger, A. and Halter-Koch, F., Non-unique factorizations. In: Algebraic, Combinatorial and Analytic Theory. Pure and Applied Mathematics 278. Chapman and Hall, Boca Raton, FL, 2006.Google Scholar
[10] Grams, A. and Warner, H., Irreducible divisors in domains of finite character. Duke Math. J. 42(1975), 271–284. doi:10.1215/S0012-7094-75-04225-8Google Scholar
[11] Hartshorne, R., Algebraic Geometry. Graduate Texts in Mathematics 52. Springer-Verlag, New York, 1977.Google Scholar
[12] Halter-Koch, F., Finiteness theorems for factorizations. Semigroup Forum 44(1992), no. 1, 1–12. doi:10.1007/BF02574329Google Scholar
[13] Kaplansky, I., A theorem on division rings. Canad. J. Math. 3(1951), 290–292.Google Scholar
[14] Kaplansky, I., Commutative Rings. Revised Edition. University of Chicago Press, Chicago, 1974.Google Scholar
[15] Malcolmson, P. and Okoh, F., Expansions of prime ideals. Rocky Mountain J. Math. 35(2005), no. 5, 1689–1706. doi:10.1216/rmjm/1181069657Google Scholar
[16] Malcolmson, P. and Okoh, F., A class of integral domains between factorial domains and IDF-domains. Houston J. Math. 32(2006), no. 2, 399–421.Google Scholar
[17] Malcolmson, P. and Okoh, F., Factorization in subalgebras of the polynomial algebra. Houston J. Math. 35(2009), no. 4, 991–1012.Google Scholar
[18] Nagata, M., Local Rings. Interscience Tracts in Pure and Applied Mathematics 13. Interscience Publishers, New York, 1962.Google Scholar
[19] Nagata, M. A type of integral extensions. J. Math. Soc. Japan 20(1968), 266–267. doi:10.2969/jmsj/02010266Google Scholar
[20] Roitman, M., Polynomial extensions of atomic domains. J. Pure Appl. Algebra 87(1993), no. 2, 187–199. doi:10.1016/0022-4049(93)90122-AGoogle Scholar