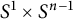A rigidity result for the product of spheres

Abstract

In this paper, we prove a rigidity result for the product metric on the product of spheres $S^1\times S^{n-1}$.

1 Introduction

Throughout this paper, we assume $n\geq 3$ . Let $g_{S^n}$ be the standard metric on the n-dimensional unit sphere $S^n$ . Answering a question of Gromov [5], Llarull [11] proved the following:

Theorem 1.1 (Theorem A in [11])

Suppose g is a Riemannian metric on $S^n$ such that its scalar curvature $R_g\geq n(n-1)=R_{g_{S^n}}$ and $g\geq g_{S^n}$ . Then we must have $g=g_{S^n}$ .

In the even-dimensional case, Listing [9] was able to generalize Theorem 1.1 as follows:

Theorem 1.2 Let $n\geq 4$ be an even integer. Moreover, suppose that g is a Riemannian metric on $S^n$ satisfying $R_g\geq (n -1) tr_g(g_{S^n})$ at each point on $S^n$ . Then g is a constant multiple of $g_{S^n}$ .

Later, rigidity results related to the scalar curvature, including compact symmetric spaces, have been obtain by other authors in [3, 4, 10, 12]. For more rigidity results involving scalar curvature, we refer the readers to the survey [1].

For any $c>0$ , let $g_c$ be the product metric given by $g_c=c\,ds^2+g_{S^{n-1}}$ on the product of spheres $S^1\times S^{n-1}$ . In this paper, we prove the following:

Theorem 1.3 Suppose g is a Riemannian metric on $S^1\times S^{n-1}$ such that:

(i) its scalar curvature $R_g\geq (n-1)(n-2)=R_{g_c}$ ,

(ii) $g\geq g_c$ , and

(iii) its Ricci curvature $Ric_g\geq 0$ .

Then g is isometric to $g_{\tilde {c}}$ for some $\tilde {c}\geq c$ .

Compared to that of Theorems 1.1 and 1.2, the assumption of Ricci curvature in Theorem 1.3 may seem to be strong. But we remark that lower bound on the Ricci curvature is assumed when rigidity result of symmetric space is studied. See Theorem 0.2 in [3].

In Section 2, we prove a conformal version of Theorem 1.3. See Corollary 2.2 for the precise statement. Note that the similar idea can be used to prove rigidity results for manifolds with boundary and for CR manifolds within a fixed conformal class. See Propositions 2.3 and 2.5.

In Section 3, we prove Theorem 1.3. We then provide examples showing that neither assumption (i) nor assumption (ii) could be dropped in Theorem 1.3. This leaves us the question whether assumption (iii) on Ricci curvature could be dropped in Theorem 1.3. While we are not able to answer it, we are able to prove a rigidity result of warped product metric without any assumption on Ricci curvature. See Theorem 3.1 for the precise statement.

2 A conformal version

As a warm-up, we will prove in this section a conformal version of Theorem 1.3. We first prove the following more general proposition.

Proposition 2.1. Suppose $(M,\tilde {g})$ is a closed (i.e., compact without boundary) Riemannian manifold such that its scalar curvature satisfies $R_{\tilde {g}}\geq 0$ and $R_{\tilde {g}}\not \equiv 0$ . If g is conformal to $\tilde {g}$ such that $g\geq \tilde {g}$ and $R_g\geq R_{\tilde {g}}$ , then $g=\tilde {g}$ .

Proof Since g is conformal to $\tilde {g}$ , we can write $g=u^{\frac {4}{n-2}}\tilde {g}$ for some $0<u\in C^\infty (M)$ . By the assumption that $g\geq \tilde {g}$ , we have

(2.1) $$ \begin{align} u\geq 1. \end{align} $$

Moreover, since $g=u^{\frac {4}{n-2}}\tilde {g}$ , it is well known that

(2.2) $$ \begin{align} -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u+R_{\tilde{g}} u=R_gu^{\frac{n+2}{n-2}}. \end{align} $$

By (2.2) and the assumption that $R_g\geq R_{\tilde {g}}$ , we find

(2.3) $$ \begin{align} \nonumber -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u &=R_gu^{\frac{n+2}{n-2}}-R_{\tilde{g}} u \\ &\geq R_{\tilde{g}}u^{\frac{n+2}{n-2}}-R_{\tilde{g}} u =R_{\tilde{g}}u^{\frac{4}{n-2}}(u-1). \end{align} $$

It follows from (2.1) and the assumption that $R_{\tilde {g}}\geq 0$ that the last term in (2.3) is nonnegative, which gives $\Delta _{\tilde {g}} u\leq 0$ in M. Since M is compact, we must have

$$ \begin{align*}u\equiv c\end{align*} $$

for some constant c. On one hand, it follows from (2.1) that $c\geq 1$ . On the other hand, by (2.2) and the assumption that $R_g\geq R_{\tilde {g}}$ , we deduce

$$ \begin{align*}R_g=R_{\tilde{g}}c^{-\frac{4}{n-2}}\geq R_{\tilde{g}}.\end{align*} $$

Since $R_{\tilde {g}}\geq 0$ and $R_{\tilde {g}}\not \equiv 0$ , we have $c\leq 1$ . That is to say, we have $c=1$ and $u\equiv 1$ , or equivalently, $g=\tilde {g}$ , as claimed.

For the product metric $g_c=c\,ds^2+g_{S^{n-1}}$ on the product of spheres $S^1\times S^{n-1}$ , the scalar curvature of $g_c$ is equal to $(n-1)(n-2)$ . Therefore, we can apply Proposition 2.1 with $(M,\tilde {g})=(S^1\times S^{n-1}, g_c)$ to get the following corollary, which is a conformal version of Theorem 1.3.

Corollary 2.2. If g is a metric on $S^1{\kern-1pt}\times{\kern-1pt} S^{n-1}$ conformal to $g_c$ such that $R_g{\kern-1pt}\geq{\kern-1pt} R_{g_c}{\kern-1pt}={\kern-1pt}(n-1) (n-2)$ and $g\geq g_c$ , then $g=g_c$ .

Note that there is no assumption on the Ricci curvature in Corollary 2.2. The idea of the proof of Proposition 2.1 can be used to prove the following:

Proposition 2.3. Suppose $(M,\tilde {g})$ is a compact Riemannian manifold with boundary $\partial M$ such that its scalar curvature satisfies $R_{\tilde {g}}\geq 0$ and $R_{\tilde {g}}\not \equiv 0$ in M and its mean curvature satisfies $H_{\tilde {g}}=0$ on $\partial M$ . If g is conformal to $\tilde {g}$ such that $g\geq \tilde {g}$ , $R_g\geq R_{\tilde {g}}$ in M, and $H_g=0$ on $\partial M$ , then $g=\tilde {g}$ .

Proof Since the proof is very similar to Proposition 2.1, we only sketch it. If we write $g=u^{\frac {4}{n-2}}\tilde {g}$ for some $0<u\in C^\infty (M)$ , we still have (2.1). Since $g=u^{\frac {4}{n-2}}\tilde {g}$ , we have (see, for example, [2])

(2.4) $$ \begin{align} \nonumber -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u+R_{\tilde{g}} u&=R_gu^{\frac{n+2}{n-2}}~~\text{ in }M, \\ \frac{2(n-1)}{n-2}\frac{\partial u}{\partial\nu_{\tilde{g}}}+H_{\tilde{g}} u&=H_g u^{\frac{n}{n-2}}~~\text{ on }\partial M. \end{align} $$

It follows from the second equation in (2.4) and the assumption that $H_g=H_{\tilde {g}}=0$ that

(2.5) $$ \begin{align} \frac{\partial u}{\partial\nu_{\tilde{g}}}=0~~\text{ on }\partial M. \end{align} $$

Following the proof of Proposition 2.1, we can conclude that

$$ \begin{align*}\Delta_{\tilde{g}}u\leq 0~~\text{ in }M.\end{align*} $$

Combining this with (2.5), we can conclude that $u\equiv c$ for some constant c. As in the proof of Proposition 2.1, we can then conclude that $u\equiv 1$ , or equivalently, $g=\tilde {g}$ .

Let $(M,g_0)$ be a closed (i.e., compact without boundary) n-dimensional Riemannian manifold such that its scalar curvature $R_{g_0}\geq 0$ and $R_{g_0}\not \equiv 0$ . Then $[0,1]\times M$ is a compact $(n+1)$ -dimensional manifold with boundary $(\{0\}\times M)\cup (\{1\}\times M)$ . Equipped with the product metric $ds^2+g_0$ , $[0,1]\times M$ has scalar curvature being equal to $R_{g_0}$ and has vanishing mean curvature. Therefore, we can apply Proposition 2.3 to get the following:

Corollary 2.4. Let $(M,g_0)$ be a closed (i.e., compact without boundary) n-dimensional Riemannian manifold such that its scalar curvature $R_{g_0}\geq 0$ and $R_{g_0}\not \equiv 0$ . If g is a metric on $[0,1]\times M$ conformal to $\tilde {g}=ds^2+g_0$ such that $g\geq \tilde {g}$ , $R_g\geq R_{\tilde {g}}$ in M, and $H_g=0$ on $\partial M$ , then $g=\tilde {g}$ .

Similarly, one can prove the following CR version of Proposition 2.1. Basic facts about CR manifolds could be found in [7] for example.

Proposition 2.5. Suppose that $(M,\tilde {\theta })$ is a compact strictly pseudoconvex CR manifold of real dimension $2N+1$ with a given contact form $\tilde {\theta }$ such that its Webster scalar curvature satisfies $R_{\tilde {\theta }}\geq 0$ and $R_{\tilde {\theta }}\not \equiv 0$ . If $\theta $ is conformal to $\tilde {\theta }$ such that $\theta \geq \tilde {\theta }$ and $R_\theta \geq R_{\tilde {\theta }}$ , then $\theta =\tilde {\theta }$ .

Proof Since $\theta $ is conformal to $\tilde {\theta }$ , we can write $\theta =u^{\frac {2}{N}}\tilde {\theta }$ for some $0<u\in C^\infty (M)$ . We then have

(2.6) $$ \begin{align} u\geq 1, \end{align} $$

since $\theta \geq \tilde {\theta }$ by assumption. Since $\theta =u^{\frac {2}{N}}\tilde {\theta }$ , we have (cf. [7])

(2.7) $$ \begin{align} -\left(2+\frac{2}{N}\right)\Delta_{\tilde{\theta}}u+R_{\tilde{\theta}}u =R_\theta u^{1+\frac{2}{N}}, \end{align} $$

where $\Delta _{\tilde {\theta }}$ is the sub-Laplacian of $\tilde {\theta }$ . Using (2.7) and the assumption that $R_\theta \geq R_{\tilde {\theta }}$ , we deduce

(2.8) $$ \begin{align} \nonumber -\left(2+\frac{2}{N}\right)\Delta_{\tilde{\theta}}u &=R_\theta u^{1+\frac{2}{N}}-R_{\tilde{\theta}}u \\ &\geq R_{\tilde{\theta}}u^{1+\frac{2}{N}}-R_{\tilde{\theta}}u = R_{\tilde{\theta}}u^{\frac{2}{N}}(u-1). \end{align} $$

From (2.7) and the assumption that $R_{\tilde {\theta }}\geq 0$ , we can see that the last term in (2.8) is nonnegative, which implies that $\Delta _{\tilde {\theta }}u\leq 0$ . Since M is compact, we have

$$ \begin{align*}u\equiv c\end{align*} $$

for some constant c. Note that $c\geq 1$ by (2.6). Note also that

$$ \begin{align*}R_\theta=R_{\tilde{\theta}}c^{-\frac{2}{N}}\geq R_{\tilde{\theta}}\end{align*} $$

by (2.7) and the assumption $R_\theta \geq R_{\tilde {\theta }}$ . Since $R_{\tilde {\theta }}\geq 0$ and $R_{\tilde {\theta }}\not \equiv 0$ , we must have $c\leq 1$ . Hence, we have $c=1$ and $u\equiv 1$ , which gives $\theta =\tilde {\theta }$ .

The unit sphere $S^{2N+1}$ in $\mathbb {C}^{N+1}=\{(z_1,...,z_{N+1})): z_i\in \mathbb {C}\}$ has a standard contact form given by

$$ \begin{align*}\theta_0=\sqrt{-1}\sum_{j=1}^{N+1}(z_jd\overline{z}_j-\overline{z}_j dz_j).\end{align*} $$

Then the Webster scalar curvature of $(S^{2N+1}, \theta _0)$ is equal to $R_{\theta _0}=N(N+1)/2$ (see, for example, [6]). The following corollary follows from Proposition 2.5 by putting $(M,\tilde {\theta })=(S^{2N+1}, \theta _0)$ :

Corollary 2.6. Let $(S^{2N+1}, \theta _0)$ be the standard CR sphere equipped with the standard contact form $\theta _0$ . If $\theta $ is conformal to $\theta _0$ such that $R_\theta \geq R_{\theta _0}=N(N+1)/2$ and $\theta \geq \theta _0$ , then $\theta =\theta _0$ .

3 Proof of Theorem 1.3

In this section, we prove Theorem 1.3.

Proof of Theorem 1.3

Consider the universal covering $\mathbb {R}\times S^{n-1}$ of $S^1\times S^{n-1}$ . The pullback of the metric g on $S^1\times S^{n-1}$ under the covering map gives a metric $\overline {g}$ on $\mathbb {R}\times S^{n-1}$ . By assumption (iii), the compact manifold $(S^1\times S^{n-1}, g)$ has nonnegative Ricci curvature. By Theorem 2.5 in Chapter I of [13], the universal covering $(\mathbb {R}\times S^{n-1},\overline {g})$ of $S^1\times S^{n-1}$ is isometric to $\mathbb {R}^k\times M$ equipped with the product metric, where M is a compact $(n-k)$ -dimensional manifold. Hence, we must have $k=1$ , and the metric $\overline {g}$ is isometric to the product metric $ds^2+\tilde {g}$ on $\mathbb {R}\times S^{n-1}$ , where $\tilde {g}$ is a metric on $S^{n-1}$ . Therefore, the metric g, which is the metric $\overline {g}$ descending on $S^1\times S^{n-1}$ through the covering map, is isometric to the product metric $\tilde {c}\,ds^2+\tilde {g}$ on $S^1\times S^{n-1}$ , where $\tilde {c}$ is a positive real number and $\tilde {g}$ is a metric on $S^{n-1}$ . As a result, up to isometry, we can assume that

(3.1) $$ \begin{align} g=\tilde{c}\,ds^2+\tilde{g}~~\text{ in }S^1\times S^{n-1}. \end{align} $$

By assumption (ii), we have $g\geq g_c$ , which together with (3.1) implies that

$$ \begin{align*}g=\tilde{c}\,ds^2+\tilde{g}\geq c\,ds^2+g_{S^{n-1}}=g_c.\end{align*} $$

From this, we have

(3.2) $$ \begin{align} \tilde{c}\geq c~~\text{ and }~~\tilde{g}\geq g_{S^{n-1}}. \end{align} $$

In view of (3.1), the scalar curvature of g is equal to the scalar of $\tilde {g}$ , i.e., $R_{\tilde {g}}=R_g.$ Combining this with assumption (i), we have

(3.3) $$ \begin{align} R_{\tilde{g}}\geq (n-1)(n-2)=R_{g_{S^{n-1}}}. \end{align} $$

In view of (3.3) and the second condition in (3.2), we can apply Llarull’s result in Theorem 1.1 to conclude that $\tilde {g}=g_{S^{n-1}}$ . Now the assertion follows from this, (3.1), and the first condition in (3.2).

The following example shows that some assumptions in Theorem 1.3 could not be dropped. Consider the product metric

$$ \begin{align*}g=ds^2+c_1g_{S^{n-1}}\end{align*} $$

on $S^1\times S^{n-1}$ , where $c_1$ is a positive constant to be chosen. Then the Ricci curvature of g is nonnegative. In particular, assumption (iii) in Theorem 1.3 is satisfied. Moreover, the scalar curvature of g is equal to

(3.4) $$ \begin{align} R_g=c_1^{-1}R_{g_{S^{n-1}}}=c_1^{-1}(n-1)(n-2). \end{align} $$

When $c_1\neq 1$ , it follows from (3.4) that g is not isometric to $g_c=cds^2+g_{S^{n-1}}$ for any $c>0$ , since the scalar curvature of $g_c$ is equal to $(n-1)(n-2)$ . Therefore, if $c_1>1$ , then

$$ \begin{align*}g=ds^2+c_1g_{S^{n-1}}>g_{1}=ds^2+g_{S^{n-1}},\end{align*} $$

i.e., assumption (ii) in Theorem 1.3 is satisfied, and by (3.4)

$$ \begin{align*}R_g=c_1^{-1}(n-1)(n-2)<(n-1)(n-2),\end{align*} $$

i.e., assumption (iii) in Theorem 1.3 is not satisfied. To conclude, we see that assumption (iii) in Theorem 1.3 cannot be dropped. On the other hand, if $c_1<1$ , then

$$ \begin{align*}g=ds^2+c_1g_{S^{n-1}}<g_{1}=ds^2+g_{S^{n-1}},\end{align*} $$

i.e., assumption (ii) in Theorem 1.3 is not satisfied, and by (3.4)

$$ \begin{align*}R_g=c_1^{-1}(n-1)(n-2)>(n-1)(n-2),\end{align*} $$

i.e., assumption (iii) in Theorem 1.3 is satisfied. From this, we see that assumption (ii) in Theorem 1.3 also cannot be dropped.

We wonder if assumption (iii) in Theorem 1.3 could be dropped. While we are not able to come up with an example, we can prove a rigidity result of warped product metric without any assumption on Ricci curvature. To this end, we consider the warped product metric

(3.5) $$ \begin{align} g=ds^2+f(s)^2\tilde{g} \end{align} $$

on $\mathbb {R}\times S^{n-1}$ , where $f>0$ and $\tilde {g}$ is a metric on $S^{n-1}$ . Let $\{e_i\}_{i=1}^n$ be an orthonormal basis with respect to g such that $e_1$ is tangent to $\mathbb {R}$ . Then the Ricci curvature of g is given by (cf. [8, Appendix A])

(3.6) $$ \begin{align} Ric_{1j}=-(n-1)\left((\log f)"+\big((\log f)'\big)^2\right)\delta_{1j} =-\frac{(n-1)f"}{f}\delta_{1j} \end{align} $$

for any $1\leq j\leq n$ , and

(3.7) $$ \begin{align} \nonumber Ric_{ij}&=\frac{1}{f^2}\widetilde{Ric}_{ij}-\left((\log f)"+(n-1)\big((\log f)'\big)^2\right)\delta_{ij} \\ &=\frac{1}{f^2}\left[\widetilde{Ric}_{ij}-\big(ff"+(n-2)(f')^2\big)\delta_{ij}\right] \end{align} $$

for any $2\leq i, j\leq n$ , where $\widetilde {Ric}$ denotes the Ricci curvature of $\tilde {g}$ . Take f to be a smooth periodic function on $\mathbb {R}$ with period $1$ . Then the warped product metric g defined in (3.5) descends to the metric $ds^2+f(s)^2\tilde {g}$ on $S^1\times S^{n-1}$ , which we still denote by g. And, (3.6) and (3.7) can still be applied. Using (3.6) and (3.7), we can compute the scalar curvature of g:

(3.8) $$ \begin{align} R_g =\frac{1}{f^2}\Big[R_{\tilde{g}}-(n-1)\big(2ff"+(n-2)(f')^2\big)\Big], \end{align} $$

where $R_{\tilde {g}}$ is the scalar curvature of $\tilde {g}$ .

Since f is a smooth periodic function on $\mathbb {R}$ , f is bounded. Let $m=\min f$ . If $g\geq g_1$ , then it follows from (3.5) that

$$ \begin{align*} g=ds^2+f(s)^2\tilde{g}\geq g_1=ds^2+g_{S^{n-1}}, \end{align*} $$

which gives

(3.9) $$ \begin{align} f(s)^2\tilde{g}\geq g_{S^{n-1}} \end{align} $$

for all $s\in \mathbb {R}$ . Take $s_0\in \mathbb {R}$ with $f(s_0)=m$ . Then (3.9) with $s=s_0$ implies that

(3.10) $$ \begin{align} \tilde{g}\geq m^{-2}g_{S^{n-1}}. \end{align} $$

On the other hand, if $R_g\geq (n-1)(n-2)$ , then it follows from (3.8) that

(3.11) $$ \begin{align} R_{\tilde{g}}\geq (n-1)\big(2ff"+(n-2)(f')^2\big)+(n-1)(n-2)f^2 \end{align} $$

for all $s\in \mathbb {R}$ . Once again, if we take $s_0\in \mathbb {R}$ with $f(s_0)=m=\min f$ , then the second derivative implies that $f"(s_0)\geq 0$ . This together with (3.11) at $s=s_0$ implies that

(3.12) $$ \begin{align} R_{\tilde{g}}\geq (n-1)(n-2)m^2. \end{align} $$

Hence, it follows from (3.10) and (3.12) that the rescaling metric $m^{2}\tilde {g}$ on $S^{n-1}$ satisfies

$$ \begin{align*}m^{2}\tilde{g}\geq g_{S^{n-1}}~~\text{ and }~~R_{m^{2}\tilde{g}}\geq (n-1)(n-2).\end{align*} $$

We can then apply Llarull’s result in Theorem 1.1 to infer that $m^2\tilde {g}=g_{S^{n-1}}$ . To conclude, we have proved the following:

Theorem 3.1 If g is a warped product metric on $S^1\times S^{n-1}$ given by (3.5) such that $g\geq g_1=ds^2+g_{S^{n-1}}$ and $R_g\geq (n-1)(n-2)$ , then $g=ds^2+m^{-2}g_{S^{n-1}}$ for some $m>0$ .