No CrossRef data available.
Published online by Cambridge University Press: 20 August 2020
We show local rigidity of hyperbolic triangle groups generated by reflections in pairs of n-dimensional subspaces of
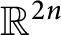 $\mathbb {R}^{2n}$
obtained by composition of the geometric representation in
$\mathbb {R}^{2n}$
obtained by composition of the geometric representation in
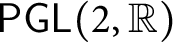 $\mathsf {PGL}(2,\mathbb {R})$
with the diagonal embeddings into
$\mathsf {PGL}(2,\mathbb {R})$
with the diagonal embeddings into
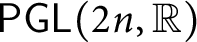 $\mathsf {PGL}(2n,\mathbb {R})$
and
$\mathsf {PGL}(2n,\mathbb {R})$
and
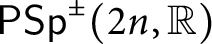 $\mathsf {PSp}^\pm (2n,\mathbb {R})$
.
$\mathsf {PSp}^\pm (2n,\mathbb {R})$
.