Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T18:28:34.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on Certain Metaplectic Groups

Published online by Cambridge University Press:  20 November 2018

Heng Sun
Heng Sun*
Affiliation:
Department of Mathematics University of Toronto Toronto, Ontario M5S 3G3
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study metaplectic coverings of the adelized group of a split connected reductive group 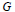$G$ over a number field 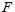$F$. Assume its derived group 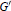${G}'$ is a simply connected simple Chevalley group. The purpose is to provide some naturally defined sections for the coverings with good properties which might be helpful when we carry some explicit calculations in the theory of automorphic forms on metaplectic groups. Specifically, we

  1. 1. construct metaplectic coverings of 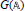$G(\mathbb{A})$ from those of 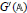${G}'\,(\mathbb{A})$;

  2. 2. for any non-archimedean place $v$, show the section for a covering of 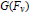$G\,({{F}_{v}})$ constructed from a Steinberg section is an isomorphism, both algebraically and topologically in an open subgroup of 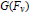$G\,({{F}_{v}})$;

  3. 3. define a global section which is a product of local sections on a maximal torus, a unipotent subgroup and a set of representatives for the Weyl group.

Keywords

20G1011G75
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 4 , 01 December 1998 , pp. 488 - 496
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Kazhdan, D. A. and Patterson, S. J., Metaplectic forms. Inst. Hautes Ètudes Sci. Publ. Math. 59 (1984), 35–142.Google Scholar
2. Kubota, T., On automorphic functions and the reciprocity law in a number field. Kinokuniya Book-Store Co., Ltd., Tokyo, 1969.Google Scholar
3. Matsumoto, H., Sur les sous-groupes arithmétiques des groupes semi-simples déployés. Ann. Sci. Ècole Norm. Sup. Sér. 4 2 (1969), 1–62.Google Scholar
4. Moeglin, C. and Waldspurger, J. L., Décomposition spectrale et séries d’Eisenstein (Une paraphrase de l’Écriture). Progr. Math. 113, Birkhäuse Verlag, 1993.Google Scholar
5. Moore, C., Group extensions of p-adic and adelic linear groups. Inst. Hautes Ètudes Sci. Publ. Math. 35 (1968), 157–222.Google Scholar
6. Nagao, H., The extensions of topological groups. Osaka J. Math. 1 (1949), 36–42.Google Scholar
7. Steinberg, R., Générateurs, relations et revĚtements de groupes algébriques. In: Colloque de Bruxelles, 1962, 113–127.Google Scholar
8. Steinberg, R., Lectures on Chevalley groups. Yale University, 1967.Google Scholar