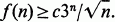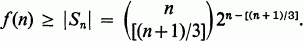Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chandra, Ashok K.
1973.
On the Solution of Moser's Problem in Four Dimensions.
Canadian Mathematical Bulletin,
Vol. 16,
Issue. 4,
p.
507.
Chvátal, V.
1973.
Edmonds polytopes and a hierarchy of combinatorial problems.
Discrete Mathematics,
Vol. 4,
Issue. 4,
p.
305.
Chandra, Ashok K
1974.
Independent permutations, as related to a problem of Moser and a theorem of Pólya.
Journal of Combinatorial Theory, Series A,
Vol. 16,
Issue. 1,
p.
111.
Sce, Michele
1981.
Geometria combinatoria e geometrie finite.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 51,
Issue. 1,
p.
77.
Guy, Richard K.
1981.
Unsolved Problems in Number Theory.
p.
110.
Chvátal, V.
2006.
Edmonds polytopes and a hierarchy of combinatorial problems.
Discrete Mathematics,
Vol. 306,
Issue. 10-11,
p.
886.
Sanders, Tom
2009.
Roth’s theorem in ℤ4n.
Analysis & PDE,
Vol. 2,
Issue. 2,
p.
211.
Polymath, D. H. J.
2010.
An Irregular Mind.
Vol. 21,
Issue. ,
p.
689.
Payne, Michael S.
and
Wood, David R.
2013.
On the General Position Subset Selection Problem.
SIAM Journal on Discrete Mathematics,
Vol. 27,
Issue. 4,
p.
1727.
Elsholtz, Christian
and
Pach, Péter Pál
2020.
Caps and progression-free sets in $${{\mathbb {Z}}}_m^n$$.
Designs, Codes and Cryptography,
Vol. 88,
Issue. 10,
p.
2133.