Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T22:47:29.721Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on a Modular Analogue of the Sato–Tate Conjecture

Published online by Cambridge University Press:  20 November 2018

Wentang Kuo
Wentang Kuo*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The original Sato–Tate Conjecture concerns the angle distribution of the eigenvalues arising from non-CM elliptic curves. In this paper, we formulate amodular analogue of the Sato–Tate Conjecture and prove that the angles arising from non-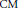$\text{CM}$ holomorphic Hecke eigenforms with non-trivial central characters are not distributed with respect to the Sate–Tatemeasure for non-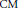$\text{CM}$ elliptic curves. Furthermore, under a reasonable conjecture, we prove that the expected distribution is uniform.

Keywords

11F0311F25L-functionsElliptic curvesSato–Tate
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 234 - 242
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Deligne, P., La conjecture de Weil. I. Inst. Hautes Études Sci. Publ. Math. 43(1974), 273–307.Google Scholar
[2] Gelbart, S. and Jacquet, H., A relation between automorphic representations of GL(2) and GL(3) . Ann. Sci. École Norm. Sup. (4) 11(1978), no. 4, 471–542.Google Scholar
[3] Godement, R. and Jacquet, H., Zeta Functions of Simple Algebras. Lecture Notes in Mathematics 260, Springer-Verlag, Berlin, 1972.Google Scholar
[4] Hecke, E., Mathematische Werke. Springer-Verlag, Göttingen, 1959.Google Scholar
[5] Jacquet, H. and Shalika, J., A non-vanishing theorem for zeta functions of GL n . Invent. Math. 38(1976), no. 1, 1–16.Google Scholar
[6] Kim, H. and Shahidi, F., Cuspidality of symmetric powers with applications. Duke Math. J. 112(2002), no. 1, 177–197.Google Scholar
[7] Labesse, J.-P. and Langlands, R. P., L-indistinguishability for SL(2) . Canad. J. Math. 31(1979), no. 4, 726–785.Google Scholar
[8] Mazur, B., Rational points of abelian varieties with values in towers of number fields. Invent. Math. 18(1972), 183–266.Google Scholar
[9] Murty, V. Kumar, On the Sato-Tate conjecture. In: Number Theory Related to Fermat's Last Theorem Progr. Math. 26, Birkhauser, Boston, MA, 1982, pp. 195–205.Google Scholar
[10] Serre, J.-P., Abelian l-adic Representations and Elliptic Curves. Benjamin, New York, 1970.Google Scholar
[11] Shahidi, F., Third symmetric power L-functions for GL(2) . Compositio Math. 70(1989), no. 3, 245–273.Google Scholar
[12] Shahidi, F., Symmetric power L-functions for GL(2) . In: Elliptic Curves and Related Topics. CRM Proc. Lecture Notes 4, American Mathematical Society, Providence, RI, 1994, pp. 159–182.Google Scholar
[13] Silverman, J., The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 106, Springer-Verlag, New York, 1986.Google Scholar