Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T19:56:45.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Injectives and Free Monads

Published online by Cambridge University Press:  20 November 2018

Harvey Wolff
Harvey Wolff*
Affiliation:
Department of Mathematics, University of Toledo, Toledo, Ohio, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ∑ be a class of maps in a category 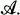An object I of 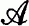is ∑-injective if is an epimorphism for all σ ∈ ∑. This paper is concerned with the question of finding “enough” S-injectives in a functorial way.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 1 , 01 March 1981 , pp. 29 - 35
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Barr, M., Coequalizers and free triples, Math. Zeit. 116 (1962), 307-322.Google Scholar
2. Beachy, J., A generalization of injectivity, Pacific J. of Math. 41 (1962), 313-327.Google Scholar
3. Cartan, H. and Eilenberg, S., Homological Algebra, Princeton University Press, Princeton, 1956.Google Scholar
4. Dubuc, E., Free Monoids, J. of Algebra. 29 (1962), 208-228.Google Scholar
5. Eilenberg, S. and Moore, J. C., Foundations of relative homological algebra, Memoirs AMS No. 55. (1962).Google Scholar
6. Freyd, P. J. and Kelly, G. M., Categories of continuous functions I, J. Pure and Appl. Algebr. 2 (1962), 169-191.Google Scholar
7. Gabriel, P. and Ulmer, F., Lokal prasentierbare kategorien, Lecture Notes in Math. 221 (Springer, Berlin) 1971.Google Scholar
8. Kelly, G. M., Quelques observations sur les démonstrations par recurrence transfinie en algèbre catégorique. Cahiers de Top. & géom. Diff. 16 (1962), 259-263.Google Scholar
9. Mitchell, B., Theory of Categories, Academic Press, New York, 1965.Google Scholar
10. Ribenboim, P., On ordered modules, J. fur die reine und angewandte Mathematik. 225 (1962), 120-146.Google Scholar
11. Wolff, H., Free monads and the orthogonal subcategory problem, to appear in J. Pure and Appl. Algebra. Google Scholar