Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T03:36:13.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Homotopy in Relational Structures

Published online by Cambridge University Press:  20 November 2018

P. J. Witbooi
P. J. Witbooi*
Affiliation:
University of the Western Cape, Private Bag X17, 7535 Bellville, South Africa e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

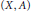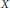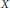The homotopy groups of a finite partially ordered set (poset) can be described entirely in the context of posets, as shown in a paper by $\text{B}$. Larose and $\text{C}$. Tardif. In this paper we describe the relative version of such a homotopy theory, for pairs $\left( X,\,A \right)$ where $X$ is a poset and $A$ is a subposet of $X$. We also prove some theorems on the relevant version of the notion of weak homotopy equivalences for maps of pairs of such objects. We work in the category of reflexive binary relational structures which contains the posets as in the work of Larose and Tardif.

Keywords

55Q0554A0518B30binary reflexive relational structurerelative homotopy groupexact sequencelocally finite spaceweak homotopy equivalence
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 2 , 01 June 2008 , pp. 310 - 320
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Adámek, J., Herrlich, H., and Strecker, G., Abstract and Concrete Categories. The Joy of Cats. John Wiley, New York, 1990.Google Scholar
[2] Alexandroff, P. S., Diskrete Räume. Matematiceskii Sbornik (N.S.) 2(1937), 501–518.Google Scholar
[3] Björner, A., Wachs, M. L., and Welker, V., Poset fiber theorems. Trans. Amer. Math. Soc. 357(2005), no. 5, 1877–1899.Google Scholar
[4] Dalmau, V., Krokhin, A., and Larose, B., Retractions onto series-parallel posets. Discrete Math. (to appear).Google Scholar
[5] Dold, A. and Thom, R., Quasifaserungen und unendliche Symmetrische Produkte. Ann. of Math. 67(1958), 239–281.Google Scholar
[6] Hardie, K. A., Salbany, S., Vermeulen, J. J. C., and Witbooi, P. J., A non-Hausdorff quaternion multiplication. Theoret. Comput. Sci. 305(2003), no. 1–3, 135–158.Google Scholar
[7] Hardie, K. A., Vermeulen, J. J. C., Witbooi, P. J., A nontrivial pairing of finite T 0 -spaces. Topology Appl. 125(2002), no. 3, 533–542.Google Scholar
[8] Larose, B. and Tardif, C., A discrete homotopy theory for binary reflexive structures. Adv. Math. 189(2004), no. 2, 268–300.Google Scholar
[9] May, J. P., Weak equivalence and quasifibrations. In: Groups of Self-Equivalences and Related Topics. Lecture Notes in Math. 1425, Springer, Berlin, 1990, pp. 91–101.Google Scholar
[10] McCord, M. C., Singular homology groups and homotopy groups of finite topological spaces. Duke Math. J. 33(1966), 465–474.Google Scholar
[11] Quillen, D., Homotopy properties of the poset of nontrivial p-subgroups of a group. Adv. in Math. 28(1978), no. 2, 101–128.Google Scholar
[12] Spanier, E. H., Algebraic Topology, McGraw-Hill, New York, 1966.Google Scholar
[13] Witbooi, P., Globalizing weak homotopy equivalences. Topology Appl. 100(2000), no. 2–3, 229–240.Google Scholar