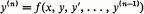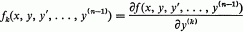Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peterson, Allan C.
1976.
An expression for the first conjugate point for an 𝑛th order nonlinear differential equation.
Proceedings of the American Mathematical Society,
Vol. 61,
Issue. 2,
p.
300.
Peterson, Allan C
1978.
Existence-uniqueness for ordinary differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 64,
Issue. 1,
p.
166.
Henderson, Johnny
1984.
Right focal point boundary value problems for ordinary differential equations and variational equations.
Journal of Mathematical Analysis and Applications,
Vol. 98,
Issue. 2,
p.
363.
Ehme, Jeffrey
and
Henderson, Johnny
1992.
Differentiation of solutions of boundary value problems with respect to boundary conditions.
Applicable Analysis,
Vol. 46,
Issue. 3-4,
p.
175.
Davis, J.M
2000.
Differentiation of solutions of lidstone boundary value problems with respect to the boundary data.
Mathematical and Computer Modelling,
Vol. 32,
Issue. 5-6,
p.
675.
Ehrke, John
Henderson, Johnny
Kunkel, Curtis
and
Sheng, Qin
2007.
Boundary data smoothness for solutions of nonlocal boundary value problems for second order differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 333,
Issue. 1,
p.
191.
Henderson, Johnny
Hopkins, Britney
Kim, Eugenie
and
Lyons, Jeffrey
2008.
Boundary data smoothness for solutions of nonlocal boundary value problems forn-th order differential equations.
Involve, a Journal of Mathematics,
Vol. 1,
Issue. 2,
p.
167.
Henderson, Johnny
and
Jiang, Xuewei
2015.
Differentiation with respect to parameters of solutions of nonlocal boundary value problems for difference equations.
Involve, a Journal of Mathematics,
Vol. 8,
Issue. 4,
p.
629.
BAXTER, LEE H.
LYONS, JEFFREY W.
and
NEUGEBAUER, JEFFREY T.
2016.
DIFFERENTIATING SOLUTIONS OF A BOUNDARY VALUE PROBLEM ON A TIME SCALE.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 1,
p.
101.
Lyons, Jeffrey
Major, Samantha
and
Seabrook, Kaitlyn
2018.
Continuous dependence and differentiating solutions of a second order boundary value problem with average value condition.
Involve, a Journal of Mathematics,
Vol. 11,
Issue. 1,
p.
95.
Jeffers, Benjamin L.
and
Lyons, Jeffrey W.
2021.
Solutions of the variational equation for an n-th
order boundary value problem with an integral boundary condition.
Involve, a Journal of Mathematics,
Vol. 14,
Issue. 1,
p.
155.
Lyons, Jeffrey W.
2024.
Differentiation of Solutions of Caputo Boundary Value Problems with Respect to Boundary Data.
Mathematics,
Vol. 12,
Issue. 12,
p.
1790.
Lyons, Jeffrey W.
2024.
CONTINUOUS DEPENDENCE ON BOUNDARY CONDITIONS FOR CAPUTO FRACTIONAL DIFFERENTIAL EQUATIONS.
Rocky Mountain Journal of Mathematics,
Vol. 54,
Issue. 3,