Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T04:44:18.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Reducing Spheres and Klein Bottles after Dehn Fillings

Published online by Cambridge University Press:  20 November 2018

Seungsang Oh
Seungsang Oh*
Affiliation:
Department of Mathematics, Korea University, 1, Anam-dong, Sungbuk-ku, Seoul 136-701, Korea, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 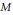$M$ be a compact, connected, orientable, irreducible 3-manifold with a torus boundary. It is known that if two Dehn fillings on 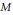$M$ along the boundary produce a reducible manifold and a manifold containing a Klein bottle, then the distance between the filling slopes is at most three. This paper gives a remarkably short proof of this result.

Keywords

57M50Dehn fillingreducibleKlein bottle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 265 - 267
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Boyer, S. and Zhang, X., Reducing Dehn filling and toroidal Dehn filling. Topology Appl. 68 (1996), 285–303.Google Scholar
[2] Gordon, C. and Luecke, J., Reducible manifolds and Dehn surgery. Topology 35 (1996), 385–409.Google Scholar
[3] Gordon, C. and Litherland, R., Incompressible planar surfaces in 3-manifolds. Topology Appl. 18 (1984), 121–144.Google Scholar
[4] Hayashi, C. and Motegi, K., Only single twists on unknots can produce composite knots. Trans. Amer. Math. Soc. 349 (1997), 4465–4479.Google Scholar
[5] Jin, G. T., Lee, S., Oh, S. and Teragaito, M., P2-reducing and toroidal Dehn fillings. Math. Proc. Camb. Phil. Soc., to appear.Google Scholar
[6] Oh, S., Dehn filling, reducible 3-manifolds, and Klein bottles. Proc. Amer. Math. Soc. 126 (1998), 289–296.Google Scholar
[7] Wu, Y. Q., Dehn fillings producing reducible manifolds and toroidal manifolds. Topology 37 (1998), 95–108.Google Scholar