Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T17:43:48.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic forms and Linkage of Quaternion Algebras

Published online by Cambridge University Press:  20 November 2018

Vatsala Krishnamani  and
Joseph Yucas
Vatsala Krishnamani
Affiliation:
Southern illinois University, CarbondaleIL 62901
Joseph Yucas
Affiliation:
Southern illinois University, CarbondaleIL 62901
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A field F satisfies n-linkage on a subset of Ḟ if whenever the quaternion algebras

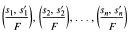
are equal in Br(F) there exist z ∈ Ḟ with

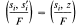
for i = 1, 2, . . ., n. This linkage of quaternion algebras is examined and its relationship to the torsion freeness of I2(F) and to the strong approximation property is investigated.

Keywords

10C0110C05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 3 , 01 September 1988 , pp. 301 - 307
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Elman, R. and Lam, T. Y., Pfister forms and K-theory of fields, J. Algebra 23 (1972), pp. 181–213.Google Scholar
2. Elman, R. and Lam, T. Y., Quadratic forms over formally real fields and Pythagorean fields, Amer. J. Math. 94 (1972), pp. 1155–1194.Google Scholar
3. Elman, R. and Lam, T. Y., Quadratic forms and the u-invariant II, Invent. Math. 21 (1973), pp. 125–137.Google Scholar
4. Elman, R. and Lam, T. Y., Classification theorems for quadratic forms over fields, Comment. Math. Helv. 49 (1974), pp. 373–381.Google Scholar
5. Kaplansky, I., Frohlich's local quadratic forms, J. Reine Angew. Math. 239 (1969), pp. 74–77.Google Scholar
6. Lam, T. Y., The algebraic theory of quadratic forms, W. A. Benjamin (1973).Google Scholar
7. Marshall, M., Abstract Witt rings, Queen papers in Pure and Applied Mathematics 57 (1980).Google Scholar