Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-11T20:53:31.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Property T and Amenable Transformation Group C*-algebras

Published online by Cambridge University Press:  20 November 2018

F. Kamalov
F. Kamalov*
Affiliation:
Mathematics Department, Canadian University of Dubai, Dubai, UAE. e-mail: firuz@cud.ac.ae
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

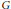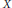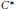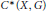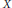It is well known that a discrete group that is both amenable and has Kazhdan’s Property $T$ must be finite. In this note we generalize this statement to the case of transformation groups. We show that if $G$ is a discrete amenable group acting on a compact Hausdorff space $X$, then the transformation group ${{C}^{*}}$-algebra ${{C}^{*}}\left( X,\,G \right)$ has Property $T$ if and only if both $X$ and 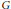$G$ are finite. Our approach does not rely on the use of tracial states on 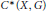${{C}^{*}}\left( X,\,G \right)$.

Keywords

46L5546L05Property TC*-algebrastransformation groupamenable
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 110 - 114
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Anantharaman-Delaroche, C., Cohomology of property T groupoids and applications. Ergodic Theory Dynam. Systems 25 (2005), no. 4, 977–1013. http://dx.doi.org/10.1017/S0143385704000884 Google Scholar
[2] Bekka, B., Property (T) for C*-algebras. Bull. London Math. Soc. 38 (2006), no. 5, 857–867. http://dx.doi.org/10.1112/S0024609306018765 Google Scholar
[3] Brown, N. P., Kazhdan's property T and C*-algebras. J. Funct. Anal. 240 (2006), no. 1, 290–296. http://dx.doi.org/10.1016/j.jfa.2006.05.003 Google Scholar
[4] Kazhdan, D. A., Connection of the dual space of a group with the structure of its closed subgroups. Funct. Anal. Appl. 1 (1967), 63–65. Google Scholar
[5] Leung, C.-W. and Ng, C.-K., Property (T) and strong property (T) for unital C*-algebras. J. Funct. Anal. 256 (2009), no. 9, 3055–3070. http://dx.doi.org/10.1016/j.jfa.2009.01.004 Google Scholar