Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T17:43:41.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of the Invariants of Solvable Lie Algebras

Published online by Cambridge University Press:  20 November 2018

J. C. Ndogmo
J. C. Ndogmo*
Affiliation:
Department of Mathematics, University of the North, Bag X1106, Sovenga 0727, South Africa, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We generalize to a field of characteristic zero certain properties of the invariant functions of the coadjoint representation of solvable Lie algebras with abelian nilradicals, previously obtained over the base field 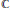$\mathbb{C}$ of complex numbers. In particular we determine their number and the restricted type of variables on which they depend. We also determine an upper bound on the maximal number of functionally independent invariants for certain families of solvable Lie algebras with arbitrary nilradicals.

Keywords

17B3022E70
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 4 , 01 December 2000 , pp. 459 - 471
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Abellanas, L. and Martinez Alonso, L., A general setting for Casimir invariants. J.Math. Phys. 16 (1975), 1580–1584.Google Scholar
[2] Carles, R., Variétés des algèbres de Lie de dimension inférieure ou égale à 7. C. R. Acad. Sci. Paris. Sér. A, B (1979), A263–A275.Google Scholar
[3] Dickson, L. E., Differential Equations from the Group Standpoint. Ann.Math. Ser. A2 25 (1924), 287–378.Google Scholar
[4] Fomenko, A. T. and Trofimov, V. V., Integrable systems on Lie algebras and symetric spaces. Gordon and Breach, New York, 1988.Google Scholar
[5] Gel’fand, I. M., The center of an infinitesimal group ring. Mat. Sbornik, 26 (1950), 103–112.Google Scholar
[6] Humphreys, J. E., Introduction to Lie algebras and representation theory. Springer-Verlag, New York, 1972.Google Scholar
[7] Ndogmo, J. C., Sur les fonctions invariantes sous l’action coadjointe d’une algèbre de Lie résoluble avec nilradical abélien. Thesis, University of Montreal, 1994.Google Scholar
[8] Ndogmo, J. C., Invariants of solvable Lie algebras of dimension k ≤ 2 modulo the nilradical. Ind. J. Math. 38 (1996), 149–160.Google Scholar
[9] Ndogmo, J. C. and Winternitz, P., Solvable Lie algebras with abelian nilradicals. J. Phys. A. Math. Gen. 27 (1994), 405–423.Google Scholar
[10] Ndogmo, J. C. and Winternitz, P., Generalized Casimir operators of solvable Lie algebras with abelian nilradicals. J. Phys. A 27 (1994), 2787–2800.Google Scholar
[11] Patera, J., Sharp, R. T., Winternitz, P. and Zassenhaus, H., Invariants of real low dimension Lie algebras. J.Math. Phys. 17 (1976), 986–994.Google Scholar
[12] Perroud, M., The fundamental invariants of inhomogeneous classical groups. J. Math. Phys. 24 (1993), 1381–1391.Google Scholar
[13] Rubin, J. L. and Winternitz, P., Solvable Lie algebras with Heisenberg ideals. J. Phys. A 26 (1993), 1123–1138.Google Scholar
[14] Racah, G., Sulla caratterizzazione delle rappresentazione irriducibili dei gruppi semisemplici di Lie. Rend. Lincei 8 (1950), 108–112.Google Scholar
[15] Racah, G., Group Theory and spectroscopy. Springer, Berlin, 1965.Google Scholar
[16] Suprunenko, D. A. and Tyshkevich, R. I., Commutative matrices. Academic Press, New York, 1968.Google Scholar
[17] Turkowski, P., Solvable Lie algebras of dimension six. J. Math. Phys. 31 (1990), 1344–1350.Google Scholar