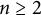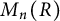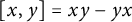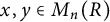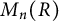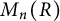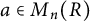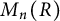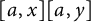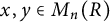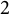1 Introduction
By the commutator of elements a and b in a ring we will always mean the additive commutator
![]() $[a,b]=ab-ba$
. The second and third named authors recently showed that if a unital ring S is generated by its commutators as an ideal, then there exists a natural number N such that every element
$[a,b]=ab-ba$
. The second and third named authors recently showed that if a unital ring S is generated by its commutators as an ideal, then there exists a natural number N such that every element
![]() $a \in S$
is a sum of N products of pairs of commutators, that is,
$a \in S$
is a sum of N products of pairs of commutators, that is,
![]() $a=\sum _{i=1}^N [b_i,c_i][d_i,e_i]$
for some
$a=\sum _{i=1}^N [b_i,c_i][d_i,e_i]$
for some
![]() $b_i,c_i,d_i,e_i\in S$
; see [Reference Gardella and ThielGT23, Theorem 3.4]. The minimal such N, denoted
$b_i,c_i,d_i,e_i\in S$
; see [Reference Gardella and ThielGT23, Theorem 3.4]. The minimal such N, denoted
![]() $\xi (S)$
, was computed or estimated for various classes of rings and
$\xi (S)$
, was computed or estimated for various classes of rings and
![]() $C^*$
-algebras. In particular, for any unital, possibly noncommutative ring R, the ring
$C^*$
-algebras. In particular, for any unital, possibly noncommutative ring R, the ring
![]() $M_n(R)$
of n-by-n matrices over R satisfies
$M_n(R)$
of n-by-n matrices over R satisfies
![]() $\xi (M_n(R)) \le 2$
for every
$\xi (M_n(R)) \le 2$
for every
![]() $n\ge 2$
; see [Reference Gardella and ThielGT23, Theorem 5.4].
$n\ge 2$
; see [Reference Gardella and ThielGT23, Theorem 5.4].
This paper is mainly concerned with the question of whether every matrix in
![]() $M_n(R)$
is actually the product of (two or more) commutators rather than a sum of double products. The fundamental case where
$M_n(R)$
is actually the product of (two or more) commutators rather than a sum of double products. The fundamental case where
![]() $R=F$
is a field was treated quite a while ago by Botha who proved that every matrix in
$R=F$
is a field was treated quite a while ago by Botha who proved that every matrix in
![]() $M_n(F)$
is a product of two commutators [Reference BothaBot97, Theorem 4.1], that is to say,
$M_n(F)$
is a product of two commutators [Reference BothaBot97, Theorem 4.1], that is to say,
![]() $\xi (M_n(F))=1$
for every field F and every
$\xi (M_n(F))=1$
for every field F and every
![]() $n\ge 2$
(for fields of characteristic
$n\ge 2$
(for fields of characteristic
![]() $0$
this was proved earlier in [Reference WuWu89]). We will be interested in more general rings.
$0$
this was proved earlier in [Reference WuWu89]). We will be interested in more general rings.
Our problem can be placed in a more general context. Over the last years, there has been a growing interest in images of noncommutative polynomials in matrix (and other) algebras. Note that the condition that
![]() $\xi (M_n(R)) =1$
can be reformulated as that the image of the polynomial
$\xi (M_n(R)) =1$
can be reformulated as that the image of the polynomial
![]() $f= [X_1,X_2][X_3,X_4]$
on
$f= [X_1,X_2][X_3,X_4]$
on
![]() $M_n(R)$
is the whole
$M_n(R)$
is the whole
![]() $M_n(R)$
. This is in the spirit of the L’vov–Kaplansky conjecture which states that the image of any multilinear polynomial on
$M_n(R)$
. This is in the spirit of the L’vov–Kaplansky conjecture which states that the image of any multilinear polynomial on
![]() $M_n(F)$
, with F a field, is a vector subspace. The aforementioned result by Botha thus shows that this is true for the polynomial f. There are only very few results treating this conjecture for arbitrary multilinear polynomials. The most well known one, obtained by Kanel–Below, Malev, and Rowen [Reference Kanel-Belov, Malev and RowenKBMR12], confirms the conjecture for the case where
$M_n(F)$
, with F a field, is a vector subspace. The aforementioned result by Botha thus shows that this is true for the polynomial f. There are only very few results treating this conjecture for arbitrary multilinear polynomials. The most well known one, obtained by Kanel–Below, Malev, and Rowen [Reference Kanel-Belov, Malev and RowenKBMR12], confirms the conjecture for the case where
![]() $n=2$
and F is quadratically closed. The majority of results, however, consider special polynomials and/or algebras different from
$n=2$
and F is quadratically closed. The majority of results, however, consider special polynomials and/or algebras different from
![]() $M_n(F)$
. We refer the reader to [Reference Kanel-Belov, Malev, Rowen and YavichKBMRY20] for a survey on this topic. Since there has been a lot of activity since its publication, we also mention a few most recent papers [Reference Brešar and VolčičBV24, Reference Fagundes and KoshlukovFK23, Reference Kaushik and SinghKS24, Reference VitasVit23] where one can find further references. It is our hope that the results and techniques in this paper, which obviously follows this line of investigation, will stimulate further research.
$M_n(F)$
. We refer the reader to [Reference Kanel-Belov, Malev, Rowen and YavichKBMRY20] for a survey on this topic. Since there has been a lot of activity since its publication, we also mention a few most recent papers [Reference Brešar and VolčičBV24, Reference Fagundes and KoshlukovFK23, Reference Kaushik and SinghKS24, Reference VitasVit23] where one can find further references. It is our hope that the results and techniques in this paper, which obviously follows this line of investigation, will stimulate further research.
Let us present the main results of this paper. In Section 2, we provide an example showing the nontriviality of our problem. The following is a simplified version of Theorem 2.2.
Example A There exist a commutative, unital ring R and a matrix
![]() $a \in M_2(R)$
that cannot be written as a product of commutators.
$a \in M_2(R)$
that cannot be written as a product of commutators.
Together with the aforementioned result from [Reference Gardella and ThielGT23], Example A shows that there exist rings R such that
![]() $\xi (M_2(R))= 2$
. This answers [Reference Gardella and ThielGT23, Question 5.7].
$\xi (M_2(R))= 2$
. This answers [Reference Gardella and ThielGT23, Question 5.7].
Section 3 is primarily devoted to matrix algebras over algebras having Bass stable rank one. The following is a combination of Theorem 3.7 and Theorem 3.9.
Theorem B Let A be a unital algebra over an infinite field, and assume that A has Bass stable rank one. Let
![]() $n\geq 3$
. Then, the following statements hold.
$n\geq 3$
. Then, the following statements hold.
-
(1) Every matrix in
 $\operatorname {\mathrm {GL}}_n(A)$
is a product of three commutators.
$\operatorname {\mathrm {GL}}_n(A)$
is a product of three commutators. -
(2) If A is right K-Hermite, then every matrix in
 $M_n(A)$
is a product of three commutators.
$M_n(A)$
is a product of three commutators.
We also prove that if A is any unital algebra over an infinite field and
![]() $n\geq 3$
, then every triangular matrix in
$n\geq 3$
, then every triangular matrix in
![]() $M_n(A)$
is a product of two commutators (Theorem 3.3). This is needed in the proof of Theorem B, but is of independent interest.
$M_n(A)$
is a product of two commutators (Theorem 3.3). This is needed in the proof of Theorem B, but is of independent interest.
Matrix rings over division rings are the topic of Section 4. The following is Theorem 4.4.
Theorem C Let D be a division ring with infinite center and let
![]() $n\geq 2$
. Then, every matrix
$n\geq 2$
. Then, every matrix
![]() $a\in M_n(D)$
is a product of two commutators.
$a\in M_n(D)$
is a product of two commutators.
The assumption that the center is infinite is unnecessary if either
![]() $n=2$
(Propostion 4.2) or if a is singular (Propostion 4.7). Its necessity in general is left open.
$n=2$
(Propostion 4.2) or if a is singular (Propostion 4.7). Its necessity in general is left open.
The final Section 5 studies a variation of the problem from the preceding sections: We consider only commutators with a fixed element (that is, values of an inner derivation), but allow for sums of their products rather than only products. The following is Theorem 5.4.
Theorem D Let F be a field, let
![]() $n\ge 2$
, and let
$n\ge 2$
, and let
![]() $a\in M_n(F)$
. Then, every matrix in
$a\in M_n(F)$
. Then, every matrix in
![]() $M_n(F)$
is a sum of matrices of the form
$M_n(F)$
is a sum of matrices of the form
![]() $[a,x][a,y]$
with
$[a,x][a,y]$
with
![]() $x,y\in M_n(F)$
if and only if the degree of the minimal polynomial of a is greater than
$x,y\in M_n(F)$
if and only if the degree of the minimal polynomial of a is greater than
![]() $2$
.
$2$
.
2 Matrices that are not products of commutators
In this section, we exhibit an example of a commutative, unital ring such that not every
![]() $2$
-by-
$2$
-by-
![]() $2$
matrix over this ring is a product of (finitely many) commutators; see Theorem 2.2.
$2$
matrix over this ring is a product of (finitely many) commutators; see Theorem 2.2.
Let C be a commutative algebra over a field F. We denote by
![]() $\operatorname {\mathrm {sl}}_2(C) \subseteq M_2(C)$
the space of trace zero matrices. Note that the commutator of any two matrices from
$\operatorname {\mathrm {sl}}_2(C) \subseteq M_2(C)$
the space of trace zero matrices. Note that the commutator of any two matrices from
![]() $M_2(C)$
belongs to
$M_2(C)$
belongs to
![]() $\operatorname {\mathrm {sl}}_2(C)$
. For the case
$\operatorname {\mathrm {sl}}_2(C)$
. For the case
![]() $C=F$
, Albert and Muckenhoupt [Reference Albert and MuckenhouptAM57] (extending earlier work of Shoda [Reference ShodaSho37, Satz 3] in characteristic
$C=F$
, Albert and Muckenhoupt [Reference Albert and MuckenhouptAM57] (extending earlier work of Shoda [Reference ShodaSho37, Satz 3] in characteristic
![]() $0$
) showed that the converse also holds, that is, a matrix over a field is a commutator if and only if it has trace zero.
$0$
) showed that the converse also holds, that is, a matrix over a field is a commutator if and only if it has trace zero.
In the following result, we consider the case where
![]() $C=F$
.
$C=F$
.
Lemma 2.1 Let
![]() $s_1,s_2,\dots ,s_n\in \operatorname {\mathrm {sl}}_2(F)$
satisfy
$s_1,s_2,\dots ,s_n\in \operatorname {\mathrm {sl}}_2(F)$
satisfy
Let
![]() $t_{1k},t_{2k},t_{3k},t_{4k}\in \operatorname {\mathrm {sl}}_2(F)$
, for
$t_{1k},t_{2k},t_{3k},t_{4k}\in \operatorname {\mathrm {sl}}_2(F)$
, for
![]() $k=1,\dots ,n$
, be any trace zero matrices, and set
$k=1,\dots ,n$
, be any trace zero matrices, and set
 $$ \begin{align*} r_1&=t_{11}s_{2}\dots s_{n} + s_{1}t_{12}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{1n},\\ r_2&=t_{21}s_{2}\dots s_{n} + s_{1}t_{22}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{2n},\\ r_3&=t_{31}s_{2}\dots s_{n} + s_{1}t_{32}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{3n},\\ r_4&=t_{41}s_{2}\dots s_{n} + s_{1}t_{42}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{4n}. \end{align*} $$
$$ \begin{align*} r_1&=t_{11}s_{2}\dots s_{n} + s_{1}t_{12}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{1n},\\ r_2&=t_{21}s_{2}\dots s_{n} + s_{1}t_{22}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{2n},\\ r_3&=t_{31}s_{2}\dots s_{n} + s_{1}t_{32}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{3n},\\ r_4&=t_{41}s_{2}\dots s_{n} + s_{1}t_{42}s_3\dots s_{n} + \dots + s_{1}\dots s_{n-1}t_{4n}. \end{align*} $$
Then,
![]() $\{r_1, r_2, r_3, r_4\}\subseteq M_2(F)$
is a linearly dependent set over F.
$\{r_1, r_2, r_3, r_4\}\subseteq M_2(F)$
is a linearly dependent set over F.
Proof Set
![]() $\mathcal {R}=\{r_1, r_2, r_3, r_4\}$
. The proof is by induction on n. If
$\mathcal {R}=\{r_1, r_2, r_3, r_4\}$
. The proof is by induction on n. If
![]() $n=1$
, then
$n=1$
, then
![]() $r_i=t_{i1}$
for all
$r_i=t_{i1}$
for all
![]() $i=1,\dots ,4$
. Thus
$i=1,\dots ,4$
. Thus
![]() $\mathcal {R} \subseteq \operatorname {\mathrm {sl}}_2(F)$
must be linearly dependent since
$\mathcal {R} \subseteq \operatorname {\mathrm {sl}}_2(F)$
must be linearly dependent since
![]() $\dim _F(\operatorname {\mathrm {sl}}_2(F))=3$
.
$\dim _F(\operatorname {\mathrm {sl}}_2(F))=3$
.
We may thus assume that the lemma is true for all positive integers less than n. If
![]() $s_1$
is invertible, then
$s_1$
is invertible, then
![]() $s_2\dots s_n=0$
and hence the induction hypothesis implies that
$s_2\dots s_n=0$
and hence the induction hypothesis implies that
![]() $s_1^{-1}\mathcal {R}$
is linearly dependent, so
$s_1^{-1}\mathcal {R}$
is linearly dependent, so
![]() $\mathcal {R}$
is linearly dependent too. We may therefore assume that
$\mathcal {R}$
is linearly dependent too. We may therefore assume that
![]() $s_1$
is not invertible, and, analogously, we may assume that
$s_1$
is not invertible, and, analogously, we may assume that
![]() $s_n$
is not invertible.
$s_n$
is not invertible.
Being 2
![]() $\times $
2 matrices with trace zero with zero determinant,
$\times $
2 matrices with trace zero with zero determinant,
![]() $s_1$
and
$s_1$
and
![]() $s_n$
have square zero, which implies that
$s_n$
have square zero, which implies that
![]() $s_1r_is_n= 0$
for all
$s_1r_is_n= 0$
for all
![]() $i=1,\dots , 4$
. If
$i=1,\dots , 4$
. If
![]() $\mathcal {R}$
was linearly independent, then it would follow that
$\mathcal {R}$
was linearly independent, then it would follow that
![]() $s_1M_2(F)s_n= \{0\}$
, which is possible only if
$s_1M_2(F)s_n= \{0\}$
, which is possible only if
![]() $s_1=0$
or
$s_1=0$
or
![]() $s_n=0$
. Assume that
$s_n=0$
. Assume that
![]() $s_1=0$
. Then,
$s_1=0$
. Then,
![]() $r_k=t_{k1}s_2\dots s_n$
for
$r_k=t_{k1}s_2\dots s_n$
for
![]() $k=1,2,3,4$
. Set
$k=1,2,3,4$
. Set
![]() $x=s_2\dots s_n$
. Then,
$x=s_2\dots s_n$
. Then,
![]() $r_1,r_2,r_3,r_4\in \mathrm {sl}_2(F)x$
, which is at most three-dimensional. Thus
$r_1,r_2,r_3,r_4\in \mathrm {sl}_2(F)x$
, which is at most three-dimensional. Thus
![]() $\mathcal {R}$
is linearly dependent, which is a contradiction. The case
$\mathcal {R}$
is linearly dependent, which is a contradiction. The case
![]() $s_n=0$
is analogous, and in either case we deduce that
$s_n=0$
is analogous, and in either case we deduce that
![]() $\mathcal {R}$
is linearly dependent.
$\mathcal {R}$
is linearly dependent.
Given a nonunital F-algebra B, recall that its (minimal) unitization is the F-algebra
![]() $C=B\oplus F$
with product given by
$C=B\oplus F$
with product given by
![]() $(a,\lambda )(b,\mu )=(\mu a + \lambda b + ab, \lambda \mu )$
for all
$(a,\lambda )(b,\mu )=(\mu a + \lambda b + ab, \lambda \mu )$
for all
![]() $a,b\in B$
and all
$a,b\in B$
and all
![]() $\lambda ,\mu \in F$
.
$\lambda ,\mu \in F$
.
Theorem 2.2 Let
![]() $C_0$
be a four-dimensional F-algebra with zero multiplication, and let
$C_0$
be a four-dimensional F-algebra with zero multiplication, and let
![]() $\{c_1,c_2,c_3,c_4\}$
be a basis for
$\{c_1,c_2,c_3,c_4\}$
be a basis for
![]() $C_0$
. Let C be the unitization of
$C_0$
. Let C be the unitization of
![]() $C_0$
. Then, the matrix
$C_0$
. Then, the matrix
![]() $a=\left [\begin {smallmatrix} c_1 & c_2\\ c_3 & c_4 \cr \end {smallmatrix} \right ]\in M_2(C)$
cannot be written as a product of elements in
$a=\left [\begin {smallmatrix} c_1 & c_2\\ c_3 & c_4 \cr \end {smallmatrix} \right ]\in M_2(C)$
cannot be written as a product of elements in
![]() $\operatorname {\mathrm {sl}}_2(C)$
. In particular, a cannot be written as a product of commutators in
$\operatorname {\mathrm {sl}}_2(C)$
. In particular, a cannot be written as a product of commutators in
![]() $M_2(C)$
.
$M_2(C)$
.
Proof Arguing by contradiction, suppose that there exist
![]() $t_1,t_2,\ldots , t_n\in \operatorname {\mathrm {sl}}_2(C)$
such that
$t_1,t_2,\ldots , t_n\in \operatorname {\mathrm {sl}}_2(C)$
such that
For each
![]() $k=1,\ldots ,n$
, there are
$k=1,\ldots ,n$
, there are
![]() $t_{1k},\ldots , t_{4k}\in M_2(F)$
and
$t_{1k},\ldots , t_{4k}\in M_2(F)$
and
![]() $t_{0k} \in F$
such that
$t_{0k} \in F$
such that
Applying the trace
![]() $\tau $
of
$\tau $
of
![]() $M_2(C)$
to the identity above, and using that
$M_2(C)$
to the identity above, and using that
![]() $t_k\in \operatorname {\mathrm {sl}}_2(C)$
yields the identity
$t_k\in \operatorname {\mathrm {sl}}_2(C)$
yields the identity
in C. Since
![]() $\{1,c_1,c_2,c_3,c_4\}$
is a linearly independent set in C, it follows that each
$\{1,c_1,c_2,c_3,c_4\}$
is a linearly independent set in C, it follows that each
![]() $t_{ik}$
belongs to
$t_{ik}$
belongs to
![]() $\operatorname {\mathrm {sl}}_2(F)$
. Moreover,
$\operatorname {\mathrm {sl}}_2(F)$
. Moreover,
![]() $a= t_1t_2\dots t_n$
implies that
$a= t_1t_2\dots t_n$
implies that
For
![]() $i,j=1,2$
, let
$i,j=1,2$
, let
![]() $e_{ij}\in M_2(C)$
be the corresponding matrix unit. Writing each matrix
$e_{ij}\in M_2(C)$
be the corresponding matrix unit. Writing each matrix
![]() $t_j$
in the basis
$t_j$
in the basis
![]() $\{1,c_1,c_2,c_3,c_4\}$
and using that
$\{1,c_1,c_2,c_3,c_4\}$
and using that
![]() $c_ic_j=0$
, the identity
$c_ic_j=0$
, the identity
![]() $a= t_1t_2\dots t_n$
can be seen to imply
$a= t_1t_2\dots t_n$
can be seen to imply
 $$ \begin{align*} e_{11}=&t_{11}t_{02}\dots t_{0n} + t_{01}t_{12}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1} t_{1n}, \\ e_{12}=&t_{21}t_{02}\dots t_{0n} + t_{01}t_{22}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1}t_{2n}, \\ e_{21}= &t_{31}t_{02}\dots t_{0n} + t_{01}t_{32}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1} t_{3n}, \\e_{22}= &t_{41}t_{02}\dots t_{0n} + t_{01}t_{42}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1} t_{4n}. \end{align*} $$
$$ \begin{align*} e_{11}=&t_{11}t_{02}\dots t_{0n} + t_{01}t_{12}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1} t_{1n}, \\ e_{12}=&t_{21}t_{02}\dots t_{0n} + t_{01}t_{22}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1}t_{2n}, \\ e_{21}= &t_{31}t_{02}\dots t_{0n} + t_{01}t_{32}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1} t_{3n}, \\e_{22}= &t_{41}t_{02}\dots t_{0n} + t_{01}t_{42}t_{03}\dots t_{0n} + \dots + t_{01}\dots t_{0\,n-1} t_{4n}. \end{align*} $$
As the set
![]() $\{e_{11}, e_{12}, e_{21}, e_{22}\}$
is linearly independent in
$\{e_{11}, e_{12}, e_{21}, e_{22}\}$
is linearly independent in
![]() $M_2(F)$
, this contradicts Lemma 2.1. Therefore the matrices
$M_2(F)$
, this contradicts Lemma 2.1. Therefore the matrices
![]() $t_1,\ldots ,t_n$
do not exist, as desired.
$t_1,\ldots ,t_n$
do not exist, as desired.
3 Matrices over algebras with Bass stable rank one
Given an algebra A over an infinite field and
![]() $n\geq 3$
, we show that every triangular n-by-n matrix over A is a product of two matrices with zero diagonal (Propostion 3.1), and hence a product of two commutators; see Theorem 3.3. As an application, we show that every element in a von Neumann algebra of type
$n\geq 3$
, we show that every triangular n-by-n matrix over A is a product of two matrices with zero diagonal (Propostion 3.1), and hence a product of two commutators; see Theorem 3.3. As an application, we show that every element in a von Neumann algebra of type
![]() $\mathrm {I}_n$
is a product of two commutators; see Example 3.4.
$\mathrm {I}_n$
is a product of two commutators; see Example 3.4.
If A has Bass stable rank one, we deduce that every invertible matrix over A is a product of three commutators; see Theorem 3.7. If A is a right K-Hermite ring with Bass stable rank one, then every matrix over A is a product of three commutators; see Theorem 3.9.
Proposition 3.1 Let R be a unital ring, and let
![]() $n \geq 3$
. Then, every upper triangular matrix in
$n \geq 3$
. Then, every upper triangular matrix in
![]() $M_n(R)$
is the product of two matrices with zero diagonals. More precisely, if
$M_n(R)$
is the product of two matrices with zero diagonals. More precisely, if
![]() $a = (a_{j,k})_{j,k} \in M_n(R)$
is upper triangular, then
$a = (a_{j,k})_{j,k} \in M_n(R)$
is upper triangular, then
![]() $a=bc$
for the matrices
$a=bc$
for the matrices
![]() $b=(b_{j,k})_{j,k} \in M_n(R)$
and
$b=(b_{j,k})_{j,k} \in M_n(R)$
and
![]() $c=(c_{j,k})_{j,k} \in M_n(R)$
given by
$c=(c_{j,k})_{j,k} \in M_n(R)$
given by
 $$\begin{align*}b_{j,k} = \begin{cases} a_{j,n}, & \text{if } j\geq 2, k=1 \\ 1, & \text{if } j=1, k=2 \\ a_{j,k-1}, & \text{if } k\geq 3 \\ 0, & \text{else} \end{cases}, \end{align*}$$
$$\begin{align*}b_{j,k} = \begin{cases} a_{j,n}, & \text{if } j\geq 2, k=1 \\ 1, & \text{if } j=1, k=2 \\ a_{j,k-1}, & \text{if } k\geq 3 \\ 0, & \text{else} \end{cases}, \end{align*}$$
and all entries of c zero except
Similarly, every lower triangular matrix in
![]() $M_n(R)$
is the product of two matrices with zero diagonals.
$M_n(R)$
is the product of two matrices with zero diagonals.
Proof The result for upper triangular matrices is proved by executing a matrix multiplication, and the result for lower triangular matrices is shown analogously. We omit the details and instead indicate the factorizations for the cases
![]() $n = 3$
and
$n = 3$
and
![]() $n = 4$
.
$n = 4$
.
In
![]() $M_3(R)$
, we have:
$M_3(R)$
, we have:
 $$ \begin{align*} \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \\ \end{pmatrix} = \begin{pmatrix} 0 & 1 & a_{12} \\ a_{23} & 0 & a_{22} \\ a_{33} & 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 & 1 \\ a_{11} & 0 & a_{13} \\ 0 & 1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \\ \end{pmatrix} = \begin{pmatrix} 0 & 1 & a_{12} \\ a_{23} & 0 & a_{22} \\ a_{33} & 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 & 1 \\ a_{11} & 0 & a_{13} \\ 0 & 1 & 0 \end{pmatrix}. \end{align*} $$
In
![]() $M_4(R)$
, we have
$M_4(R)$
, we have
 $$ \begin{align*} \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ 0 & a_{22} & a_{23} & a_{24} \\ 0 & 0 & a_{33} & a_{34} \\ 0 & 0 & 0 & a_{44} \end{pmatrix} = \begin{pmatrix} 0 & 1 & a_{12} & a_{13} \\ a_{24} & 0 & a_{22} & a_{23} \\ a_{34} & 0 & 0 & a_{33} \\ a_{44} & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 1 \\ a_{11} & 0 & 0 & a_{14} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ 0 & a_{22} & a_{23} & a_{24} \\ 0 & 0 & a_{33} & a_{34} \\ 0 & 0 & 0 & a_{44} \end{pmatrix} = \begin{pmatrix} 0 & 1 & a_{12} & a_{13} \\ a_{24} & 0 & a_{22} & a_{23} \\ a_{34} & 0 & 0 & a_{33} \\ a_{44} & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 1 \\ a_{11} & 0 & 0 & a_{14} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}. \end{align*} $$
The next result is well known, but we could not locate a precise reference.
Lemma 3.2 Let
![]() $n \geq 2$
, and let R be a unital ring containing central elements
$n \geq 2$
, and let R be a unital ring containing central elements
![]() $a_1,\ldots ,a_n \in R$
such that the pairwise differences
$a_1,\ldots ,a_n \in R$
such that the pairwise differences
![]() $a_j-a_k$
for
$a_j-a_k$
for
![]() $j \neq k$
are invertible in R. Then every n-by-n matrix with zero diagonal is a commutator in
$j \neq k$
are invertible in R. Then every n-by-n matrix with zero diagonal is a commutator in
![]() $M_n(R)$
.
$M_n(R)$
.
Proof Consider the diagonal matrix a with diagonal entries
![]() $a_1,\ldots ,a_n$
. Given a matrix
$a_1,\ldots ,a_n$
. Given a matrix
![]() $b=(b_{jk})_{j,k} \in M_n(R)$
, the commutator
$b=(b_{jk})_{j,k} \in M_n(R)$
, the commutator
![]() $[a,b]$
is the matrix
$[a,b]$
is the matrix
![]() $(c_{jk})_{j,k}$
with entries
$(c_{jk})_{j,k}$
with entries
![]() $c_{jk}=(a_j-a_k)b_{jk}$
for
$c_{jk}=(a_j-a_k)b_{jk}$
for
![]() $j,k=1,\ldots ,n$
. We illustrate the case
$j,k=1,\ldots ,n$
. We illustrate the case
![]() $n=3$
:
$n=3$
:
 $$ \begin{align*} &\left[ \begin{pmatrix} a_{1} & 0 & 0 \\ 0 & a_{2} & 0 \\ 0 & 0 & a_{3} \\ \end{pmatrix}, \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \\ \end{pmatrix} \right] \\ &\qquad\qquad\qquad= \begin{pmatrix} 0 & (a_1-a_2)b_{12} & (a_1-a_3)b_{13} \\ (a_2-a_1)b_{21} & 0 & (a_2-a_3)b_{23} \\ (a_3-a_1)b_{31} & (a_3-a_2)b_{32} & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} &\left[ \begin{pmatrix} a_{1} & 0 & 0 \\ 0 & a_{2} & 0 \\ 0 & 0 & a_{3} \\ \end{pmatrix}, \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \\ \end{pmatrix} \right] \\ &\qquad\qquad\qquad= \begin{pmatrix} 0 & (a_1-a_2)b_{12} & (a_1-a_3)b_{13} \\ (a_2-a_1)b_{21} & 0 & (a_2-a_3)b_{23} \\ (a_3-a_1)b_{31} & (a_3-a_2)b_{32} & 0 \end{pmatrix}. \end{align*} $$
Now, given a matrix
![]() $c = (c_{jk})_{j,k} \in M_n(R)$
with zero diagonal, consider the matrix b with entries
$c = (c_{jk})_{j,k} \in M_n(R)$
with zero diagonal, consider the matrix b with entries
![]() $b_{jj} = 0$
for
$b_{jj} = 0$
for
![]() $j=1,\ldots ,n$
and
$j=1,\ldots ,n$
and
![]() $b_{jk}:=(a_j-a_k)^{-1}c_{jk}$
for
$b_{jk}:=(a_j-a_k)^{-1}c_{jk}$
for
![]() $j \neq k$
. Then
$j \neq k$
. Then
![]() $c=[a,b]$
.
$c=[a,b]$
.
Theorem 3.3 Let A be a unital algebra over an infinite field, and let
![]() $n \geq 3$
. Then every upper (lower) triangular matrix in
$n \geq 3$
. Then every upper (lower) triangular matrix in
![]() $M_n(A)$
is the product of two commutators.
$M_n(A)$
is the product of two commutators.
Proof By Propostion 3.1, every triangular matrix is the product of two matrices with zero diagonal. Since A is an algebra over an infinite field, the assumptions of Lemma 3.2 are satisfied and it follows that every matrix over A with zero diagonal is a commutator.
For a topological space X, we write
![]() $C(X)$
for the algebra of all continuous functions
$C(X)$
for the algebra of all continuous functions
![]() $X\to \mathbb {C}$
endowed with pointwise operations. Recall that a space X is said to be extremally disconnected (also called a Stonean space), if the closure of every open set in X is open (and hence clopen).
$X\to \mathbb {C}$
endowed with pointwise operations. Recall that a space X is said to be extremally disconnected (also called a Stonean space), if the closure of every open set in X is open (and hence clopen).
Example 3.4 Let
![]() $n \geq 3$
, and let A be an
$n \geq 3$
, and let A be an
![]() $AW^*$
-algebra of type
$AW^*$
-algebra of type
![]() $\mathrm {I}_n$
in the sense of [Reference BerberianBer72, Definition 18.2]. (This includes all von Neumann algebras of type
$\mathrm {I}_n$
in the sense of [Reference BerberianBer72, Definition 18.2]. (This includes all von Neumann algebras of type
![]() $\mathrm {I}_n$
, that is, von Neumann algebras such that every irreducible representation acts on a Hilbert space of dimension n.) We will argue that every element in A is a product of two commutators.
$\mathrm {I}_n$
, that is, von Neumann algebras such that every irreducible representation acts on a Hilbert space of dimension n.) We will argue that every element in A is a product of two commutators.
It is a standard fact in C*-algebra theory that there is an extrem disconnected compact Hausdorff space X such that
![]() $A \cong M_n(C(X))$
. Given
$A \cong M_n(C(X))$
. Given
![]() $a \in M_n(C(X))$
, by a result of Deckard and Pearcy [Reference Deckard and PearcyDP63, Theorem 2] there exists a unitary
$a \in M_n(C(X))$
, by a result of Deckard and Pearcy [Reference Deckard and PearcyDP63, Theorem 2] there exists a unitary
![]() $u \in M_n(C(X))$
such that
$u \in M_n(C(X))$
such that
![]() $uau^*$
is upper triangular. (A more conceptual proof of this result was given in [Reference AzoffAzo74, Corollary 6].) If
$uau^*$
is upper triangular. (A more conceptual proof of this result was given in [Reference AzoffAzo74, Corollary 6].) If
![]() $n \geq 3$
, then it follows from Theorem 3.3 that
$n \geq 3$
, then it follows from Theorem 3.3 that
![]() $uau^*$
is a product of two commutators, and consequently so is a itself.
$uau^*$
is a product of two commutators, and consequently so is a itself.
The result also holds for
![]() $n=2$
, and in fact for arbitrary von Neumann algebras of type
$n=2$
, and in fact for arbitrary von Neumann algebras of type
![]() $\mathrm {I}$
, but the proof is more complicated since one needs to control the norm of the elements going into the commutators. This will appear in forthcoming work of the second and third named authors; see [Reference Gardella and ThielGT24].
$\mathrm {I}$
, but the proof is more complicated since one needs to control the norm of the elements going into the commutators. This will appear in forthcoming work of the second and third named authors; see [Reference Gardella and ThielGT24].
We say that a matrix
![]() $(a_{jk})_{j,k} \in M_n(R)$
has zero trace if
$(a_{jk})_{j,k} \in M_n(R)$
has zero trace if
![]() $a_{11} + \ldots + a_{nn} = 0$
. The following result is well known; see, for example, [Reference Kaufman and PasleyKP14, Theorem 4].
$a_{11} + \ldots + a_{nn} = 0$
. The following result is well known; see, for example, [Reference Kaufman and PasleyKP14, Theorem 4].
Theorem 3.5 Let R be a unital ring, and
![]() $n \geq 2$
. Then every triangular matrix in
$n \geq 2$
. Then every triangular matrix in
![]() $M_n(R)$
with zero trace is a commutator.
$M_n(R)$
with zero trace is a commutator.
A unital ring R is said to have Bass stable rank one if for all
![]() $a,b \in R$
such that
$a,b \in R$
such that
![]() $R = Ra+Rb$
, there exists
$R = Ra+Rb$
, there exists
![]() $c \in R$
such that
$c \in R$
such that
![]() $R = R(a+cb)$
. In other words, whenever a and b generate R as a left ideal, then there exists an element
$R = R(a+cb)$
. In other words, whenever a and b generate R as a left ideal, then there exists an element
![]() $c\in R$
such that
$c\in R$
such that
![]() $a+cb$
is left invertible. For more details and an overview on the theory of Bass stable rank, we refer to [Reference ChenChe11, Reference VasersteinVas84].
$a+cb$
is left invertible. For more details and an overview on the theory of Bass stable rank, we refer to [Reference ChenChe11, Reference VasersteinVas84].
Two matrices
![]() $a,b \in M_n(R)$
over a unital ring R are said to be similar if
$a,b \in M_n(R)$
over a unital ring R are said to be similar if
![]() $a = vbv^{-1}$
for some
$a = vbv^{-1}$
for some
![]() $v \in \operatorname {\mathrm {GL}}_n(R)$
. In [Reference Vaserstein and WhelandVW90], Vaserstein and Wheland showed that every invertible matrix over a ring with Bass stable rank one is a product of three triangular matrices, and similar to a product of two triangular matrices. Combined with Theorem 3.3, one can immediately deduce that invertible matrices over suitable rings are products of four commutators. Using a more refined argument, we show that products of three commutators suffice; see Theorem 3.7.
$v \in \operatorname {\mathrm {GL}}_n(R)$
. In [Reference Vaserstein and WhelandVW90], Vaserstein and Wheland showed that every invertible matrix over a ring with Bass stable rank one is a product of three triangular matrices, and similar to a product of two triangular matrices. Combined with Theorem 3.3, one can immediately deduce that invertible matrices over suitable rings are products of four commutators. Using a more refined argument, we show that products of three commutators suffice; see Theorem 3.7.
Lemma 3.6 Let R be a unital ring of Bass stable rank one, let
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $a \in \operatorname {\mathrm {GL}}_n(R)$
. Then there exist
$a \in \operatorname {\mathrm {GL}}_n(R)$
. Then there exist
![]() $b,c \in \operatorname {\mathrm {GL}}_n(R)$
such that b is lower triangular, c is upper triangular with all diagonal entries equal to
$b,c \in \operatorname {\mathrm {GL}}_n(R)$
such that b is lower triangular, c is upper triangular with all diagonal entries equal to
![]() $1$
, and a is similar to
$1$
, and a is similar to
![]() $bc$
.
$bc$
.
Proof By [Reference Vaserstein and WhelandVW90, Theorem 1], there exist
![]() $x,y,z \in \operatorname {\mathrm {GL}}_n(R)$
such that
$x,y,z \in \operatorname {\mathrm {GL}}_n(R)$
such that
![]() $a = xyz$
, and such that x and z are lower triangular, and y is upper triangular. From the proof of [Reference Vaserstein and WhelandVW90, Theorem 1] we see that we can arrange that y and z have all diagonal entries equal to
$a = xyz$
, and such that x and z are lower triangular, and y is upper triangular. From the proof of [Reference Vaserstein and WhelandVW90, Theorem 1] we see that we can arrange that y and z have all diagonal entries equal to
![]() $1$
. Set
$1$
. Set
![]() $b := zx$
and
$b := zx$
and
![]() $c := y$
. Then b is lower triangular, and c is upper triangular with all diagonal entries equal to
$c := y$
. Then b is lower triangular, and c is upper triangular with all diagonal entries equal to
![]() $1$
. Further, a is similar to the matrix
$1$
. Further, a is similar to the matrix
![]() $zaz^{-1} = (zx) y = bc$
.
$zaz^{-1} = (zx) y = bc$
.
Theorem 3.7 Let A be a unital algebra over an infinite field, and assume that A has Bass stable rank one. Then, for
![]() $n \geq 3$
, every matrix in
$n \geq 3$
, every matrix in
![]() $\operatorname {\mathrm {GL}}_n(A)$
is a product of three commutators.
$\operatorname {\mathrm {GL}}_n(A)$
is a product of three commutators.
Proof Let
![]() $a \in \operatorname {\mathrm {GL}}_n(A)$
. Use Lemma 3.6 to find
$a \in \operatorname {\mathrm {GL}}_n(A)$
. Use Lemma 3.6 to find
![]() $b,c \in \operatorname {\mathrm {GL}}_n(A)$
such that b is lower triangular, c is upper triangular with all diagonal entries equal to
$b,c \in \operatorname {\mathrm {GL}}_n(A)$
such that b is lower triangular, c is upper triangular with all diagonal entries equal to
![]() $1$
, and a is similar to
$1$
, and a is similar to
![]() $bc$
. It suffices to show that
$bc$
. It suffices to show that
![]() $bc$
is a product of three commutators, since then so is a.
$bc$
is a product of three commutators, since then so is a.
Since A is an algebra over an infinite field, we can find invertible elements
![]() $\lambda _1,\ldots ,\lambda _n \in A$
such that
$\lambda _1,\ldots ,\lambda _n \in A$
such that
![]() $\lambda _1+\ldots +\lambda _n = 0$
. Let
$\lambda _1+\ldots +\lambda _n = 0$
. Let
![]() $e \in M_n(A)$
denote the diagonal matrix with diagonal entries
$e \in M_n(A)$
denote the diagonal matrix with diagonal entries
![]() $\lambda _1,\ldots ,\lambda _n$
. Then,
$\lambda _1,\ldots ,\lambda _n$
. Then,
![]() $ec$
is upper triangular with diagonal
$ec$
is upper triangular with diagonal
![]() $\lambda _1,\ldots ,\lambda _n$
. Thus,
$\lambda _1,\ldots ,\lambda _n$
. Thus,
![]() $ec$
has trace zero, and is therefore a commutator by Theorem 3.5. Further,
$ec$
has trace zero, and is therefore a commutator by Theorem 3.5. Further,
![]() $be^{-1}$
is lower triangular (not necessarily with trace zero), and therefore is a product of two commutators by Theorem 3.3. Thus,
$be^{-1}$
is lower triangular (not necessarily with trace zero), and therefore is a product of two commutators by Theorem 3.3. Thus,
![]() $bc=(be^{-1})(ec)$
is a product of three commutators.
$bc=(be^{-1})(ec)$
is a product of three commutators.
There are different notions of a “left (right) Hermite ring” in the literature, some meaning that every finitely generated, stably free left (right) R-module is free (see, for example, [Reference LamLam06, Definition I.4.6]), and some referring to the notion studied by Kaplansky in [Reference KaplanskyKap49]. Following Lam, [Reference LamLam06, Definition I.4.23], we say that a (not necessarily commutative) ring R is right K-Hermite (the “K” standing for Kaplansky) if for every
![]() $1$
-by-
$1$
-by-
![]() $2$
matrix
$2$
matrix
![]() $\begin {pmatrix} x & y \end {pmatrix} \in M_{1,2}(R)$
there exists
$\begin {pmatrix} x & y \end {pmatrix} \in M_{1,2}(R)$
there exists
![]() $Q \in \operatorname {\mathrm {GL}}_2(R)$
such that
$Q \in \operatorname {\mathrm {GL}}_2(R)$
such that
![]() $\begin {pmatrix} x & y \end {pmatrix}Q = \begin {pmatrix} z & 0 \end {pmatrix}$
for some
$\begin {pmatrix} x & y \end {pmatrix}Q = \begin {pmatrix} z & 0 \end {pmatrix}$
for some
![]() $z \in R$
. Equivalently, for every rectangular matrix
$z \in R$
. Equivalently, for every rectangular matrix
![]() $a \in M_{m,n}(R)$
there exists an invertible matrix
$a \in M_{m,n}(R)$
there exists an invertible matrix
![]() $v \in M_n(R)$
such that
$v \in M_n(R)$
such that
![]() $av$
is lower triangular; see [Reference KaplanskyKap49, Theorem 3.5]. Similarly, a ring R is left K-Hermite if for every rectangular matrix
$av$
is lower triangular; see [Reference KaplanskyKap49, Theorem 3.5]. Similarly, a ring R is left K-Hermite if for every rectangular matrix
![]() $a \in M_{m,n}(R)$
there exists an invertible matrix
$a \in M_{m,n}(R)$
there exists an invertible matrix
![]() $w \in M_m(R)$
such that
$w \in M_m(R)$
such that
![]() $wa$
is upper triangular.
$wa$
is upper triangular.
The next result is analogous to Lemma 3.6, with the only difference that we obtain a result for all matrices (not only invertible matrices), and the lower triangular matrix b may thus not be invertible.
Lemma 3.8 Let R be a unital, right K-Hermite ring of Bass stable rank one, let
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $a \in M_n(R)$
. Then there exist
$a \in M_n(R)$
. Then there exist
![]() $b,c \in M_n(R)$
such that b is lower triangular, c is upper triangular with all diagonal entries equal to
$b,c \in M_n(R)$
such that b is lower triangular, c is upper triangular with all diagonal entries equal to
![]() $1$
, and a is similar to
$1$
, and a is similar to
![]() $bc$
.
$bc$
.
Proof By [Reference KaplanskyKap49, Theorem 3.5], there exist a lower triangular matrix
![]() $x \in M_n(R)$
and
$x \in M_n(R)$
and
![]() $y \in \operatorname {\mathrm {GL}}_n(R)$
such that
$y \in \operatorname {\mathrm {GL}}_n(R)$
such that
![]() $a = xy$
. We now apply [Reference Vaserstein and WhelandVW90, Theorem 1] for y and obtain
$a = xy$
. We now apply [Reference Vaserstein and WhelandVW90, Theorem 1] for y and obtain
![]() $u,v,w \in \operatorname {\mathrm {GL}}_n(R)$
such that
$u,v,w \in \operatorname {\mathrm {GL}}_n(R)$
such that
![]() $y = uvw$
, and such that u and w are lower triangular, and v is upper triangular. From the proof of [Reference Vaserstein and WhelandVW90, Theorem 1] we see that we can arrange that v and w have all diagonal entries equal to
$y = uvw$
, and such that u and w are lower triangular, and v is upper triangular. From the proof of [Reference Vaserstein and WhelandVW90, Theorem 1] we see that we can arrange that v and w have all diagonal entries equal to
![]() $1$
.
$1$
.
Set
![]() $b := wxu$
and
$b := wxu$
and
![]() $c := v$
. Then, b is lower triangular, and c is upper triangular with all diagonal entries equal to
$c := v$
. Then, b is lower triangular, and c is upper triangular with all diagonal entries equal to
![]() $1$
. Further, a is similar to the matrix
$1$
. Further, a is similar to the matrix
![]() $waw^{-1} = w(xuvw)w^{-1} = (wxu)v = bc$
.
$waw^{-1} = w(xuvw)w^{-1} = (wxu)v = bc$
.
Theorem 3.9 Let A be a unital algebra over an infinite field, and assume that A is right K-Hermite and has Bass stable rank one. Then for
![]() $n \geq 3$
, every matrix in
$n \geq 3$
, every matrix in
![]() $M_n(A)$
is a product of three commutators.
$M_n(A)$
is a product of three commutators.
Proof This is analogous to the proof of Theorem 3.7.
Question 3.10 Can the assumption that A is an algebra over an infinite field be removed in Theorem 3.7 or Theorem 3.9? Do these results hold for
![]() $n=2$
?
$n=2$
?
Remark 3.11 Chen and Chen showed in [Reference Chen and ChenCC04, Theorem 2.2] that a unital ring R is right K-Hermite and has Bass stable rank one if and only if every matrix
![]() $a \in M_n(R)$
admits a factorization
$a \in M_n(R)$
admits a factorization
![]() $a=bcd$
in
$a=bcd$
in
![]() $M_n(R)$
with b and d lower triangular, c upper triangular and all diagonal entries of c and d equal to
$M_n(R)$
with b and d lower triangular, c upper triangular and all diagonal entries of c and d equal to
![]() $1$
.
$1$
.
Let us point out a few instances to which the above results are applicable. The first one is extremely easy, but we will need it in the next section.
Example 3.12 Every division ring D is right K-Hermite and has Bass stable rank one. The latter is obvious since D has no proper nonzero left ideals. To prove the former, take
![]() $x,y\in D$
. We want to find an invertible matrix
$x,y\in D$
. We want to find an invertible matrix
![]() $Q\in M_2(D)$
such that
$Q\in M_2(D)$
such that
![]() $\begin {pmatrix} x & y \end {pmatrix}Q=\begin {pmatrix} z & 0 \end {pmatrix}$
for some
$\begin {pmatrix} x & y \end {pmatrix}Q=\begin {pmatrix} z & 0 \end {pmatrix}$
for some
![]() $z\in D$
. If
$z\in D$
. If
![]() $x\neq 0$
, one may take
$x\neq 0$
, one may take ![]() . If
. If
![]() $x=0$
, one may take
$x=0$
, one may take ![]() . It follows that D is right K-Hermite.
. It follows that D is right K-Hermite.
The next example is more general.
Example 3.13 A unital ring is said to be (von Neumann) regular if for every
![]() $x \in R$
there exists
$x \in R$
there exists
![]() $y \in R$
such that
$y \in R$
such that
![]() $x = xyx$
. If one can always arrange y to be invertible, then R is said to be unit-regular. We refer to [Reference GoodearlGoo79] for more details.
$x = xyx$
. If one can always arrange y to be invertible, then R is said to be unit-regular. We refer to [Reference GoodearlGoo79] for more details.
A regular ring has Bass stable rank one if and only if it is unit-regular; see [Reference GoodearlGoo79, Proposition 4.12]. Further, every unit-regular ring is right K-Hermite; this follows from [Reference Menal and MoncasiMM82, Theorem 9] as noted in the introduction of [Reference Ara, Goodearl, O’Meara and PardoAGOP97].
Thus, if R is a unit-regular ring that is an algebra over an infinite field, and
![]() $n \geq 3$
, then every matrix in
$n \geq 3$
, then every matrix in
![]() $M_n(R)$
is a product of three commutators by Theorem 3.9.
$M_n(R)$
is a product of three commutators by Theorem 3.9.
Example 3.14 A unital
![]() $C^*$
-algebra A is said to have stable rank one if
$C^*$
-algebra A is said to have stable rank one if
![]() $\operatorname {\mathrm {GL}}(A)$
is norm-dense in A; see [Reference RieffelRie83]. By [Reference Herman and VasersteinHV84], A has stable rank one if and only if A has Bass stable rank one (as a ring). Further, every
$\operatorname {\mathrm {GL}}(A)$
is norm-dense in A; see [Reference RieffelRie83]. By [Reference Herman and VasersteinHV84], A has stable rank one if and only if A has Bass stable rank one (as a ring). Further, every
![]() $C^*$
-algebra is an algebra over the infinite field of complex numbers. Therefore, Theorem 3.7 applies to invertible matrices of size at least
$C^*$
-algebra is an algebra over the infinite field of complex numbers. Therefore, Theorem 3.7 applies to invertible matrices of size at least
![]() $3$
-by-
$3$
-by-
![]() $3$
over
$3$
over
![]() $C^*$
-algebras of stable rank one. In some cases, one has
$C^*$
-algebras of stable rank one. In some cases, one has
![]() $A \cong M_n(B)$
for some
$A \cong M_n(B)$
for some
![]() $n \geq 3$
and some other
$n \geq 3$
and some other
![]() $C^*$
-algebra B (which then automatically has stable rank one as well) and then Theorem 3.7 applies to invertible elements in A itself. For example, every invertible element in a UHF-algebra is a product of three commutators.
$C^*$
-algebra B (which then automatically has stable rank one as well) and then Theorem 3.7 applies to invertible elements in A itself. For example, every invertible element in a UHF-algebra is a product of three commutators.
Many naturally occurring simple, unital
![]() $C^*$
-algebras have stable rank one. This includes all finite, nuclear, classifiable
$C^*$
-algebras have stable rank one. This includes all finite, nuclear, classifiable
![]() $C^*$
-algebras [Reference RèrdamRør04]; many finite, nuclear, non-classifiable
$C^*$
-algebras [Reference RèrdamRør04]; many finite, nuclear, non-classifiable
![]() $C^*$
-algebras [Reference Elliott, Ho and TomsEHT09, Reference TomsTom08, Reference VilladsenVil98]; reduced group
$C^*$
-algebras [Reference Elliott, Ho and TomsEHT09, Reference TomsTom08, Reference VilladsenVil98]; reduced group
![]() $C^*$
-algebras of free products [Reference Dykema, Haagerup and RèrdamDHR97]; and crossed products of minimal homeomorphisms on infinite, compact, and metric spaces [Reference Alboiu and LutleyAL22].
$C^*$
-algebras of free products [Reference Dykema, Haagerup and RèrdamDHR97]; and crossed products of minimal homeomorphisms on infinite, compact, and metric spaces [Reference Alboiu and LutleyAL22].
The comparison theory of positive elements and Hilbert modules is particularly well-developed for
![]() $C^*$
-algebras of stable rank one [Reference Antoine, Perera, Robert and ThielAPRT22, Reference ThielThi20].
$C^*$
-algebras of stable rank one [Reference Antoine, Perera, Robert and ThielAPRT22, Reference ThielThi20].
4 Matrices over division rings
In this section, we show that every matrix over a division ring with infinite center is a product of two commutators; see Theorem 4.4. We also show that every singular matrix over an arbitrary division ring is a product of two commutators; see Propostion 4.7.
Lemma 4.1 Let D be a division ring, and let
![]() $r,s,t \in D$
. Then, the matrix
$r,s,t \in D$
. Then, the matrix ![]() is a commutator in
is a commutator in
![]() $M_2(D)$
. More precisely, there exist
$M_2(D)$
. More precisely, there exist
![]() $b \in \operatorname {\mathrm {GL}}_2(D)$
and
$b \in \operatorname {\mathrm {GL}}_2(D)$
and
![]() $c \in M_2(D)$
such that
$c \in M_2(D)$
such that
![]() $a = [b,c]$
.
$a = [b,c]$
.
Proof Case 1: We have
![]() $r=0$
and
$r=0$
and
![]() $s,t \neq 0$
. Then,
$s,t \neq 0$
. Then,
 $$ \begin{align*} \begin{pmatrix} 0 & s \\ t & 0 \end{pmatrix} = \left[ \begin{pmatrix} 0 & -s \\ t & 0 \end{pmatrix}, \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} \right] \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0 & s \\ t & 0 \end{pmatrix} = \left[ \begin{pmatrix} 0 & -s \\ t & 0 \end{pmatrix}, \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} \right] \end{align*} $$
and the matrix ![]() is invertible.
is invertible.
Case 2: We have
![]() $s=0$
. Then,
$s=0$
. Then,
 $$ \begin{align*} \begin{pmatrix} r & 0 \\ t & -r \end{pmatrix} = \left[ \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix} 0 & -r \\ 0 & -t \end{pmatrix} \right] \end{align*} $$
$$ \begin{align*} \begin{pmatrix} r & 0 \\ t & -r \end{pmatrix} = \left[ \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix} 0 & -r \\ 0 & -t \end{pmatrix} \right] \end{align*} $$
and the matrix ![]() is invertible.
is invertible.
Case 3: We have
![]() $t=0$
. This is analogous to case 2.
$t=0$
. This is analogous to case 2.
Case 4: We have
![]() $r,s,t \neq 0$
. Then,
$r,s,t \neq 0$
. Then,
 $$ \begin{align*} \begin{pmatrix} r & s \\ t & -r \end{pmatrix} = \left[ \begin{pmatrix} 0 & -srt^{-1} \\ r & 0 \end{pmatrix}, \begin{pmatrix} 0 & -1 \\ 0 & -tr^{-1} \end{pmatrix} \right] \end{align*} $$
$$ \begin{align*} \begin{pmatrix} r & s \\ t & -r \end{pmatrix} = \left[ \begin{pmatrix} 0 & -srt^{-1} \\ r & 0 \end{pmatrix}, \begin{pmatrix} 0 & -1 \\ 0 & -tr^{-1} \end{pmatrix} \right] \end{align*} $$
and the matrix ![]() is invertible.
is invertible.
Next, we consider arbitrary
![]() $2$
-by-
$2$
-by-
![]() $2$
matrices over a division ring.
$2$
matrices over a division ring.
Proposition 4.2 Let D be a division ring, and let
![]() $a \in M_2(D)$
. Then, there exist
$a \in M_2(D)$
. Then, there exist
![]() $b,c,d,e \in M_2(D)$
such that
$b,c,d,e \in M_2(D)$
such that
![]() $a=[b,c][d,e]$
, and such that
$a=[b,c][d,e]$
, and such that
![]() $[b,c]$
and d are invertible. In particular, every matrix in
$[b,c]$
and d are invertible. In particular, every matrix in
![]() $M_2(D)$
is a product of two commutators.
$M_2(D)$
is a product of two commutators.
Proof Let ![]() .
.
Case 1: We have
![]() $s,t \neq 0$
. Then,
$s,t \neq 0$
. Then,
 $$ \begin{align*} a = \begin{pmatrix} r & s \\ t & u \end{pmatrix} = \begin{pmatrix} 0 & -st^{-1} \\ 1 & 0 \end{pmatrix} \begin{pmatrix} t & u \\ -ts^{-1}r & -t \end{pmatrix} \end{align*} $$
$$ \begin{align*} a = \begin{pmatrix} r & s \\ t & u \end{pmatrix} = \begin{pmatrix} 0 & -st^{-1} \\ 1 & 0 \end{pmatrix} \begin{pmatrix} t & u \\ -ts^{-1}r & -t \end{pmatrix} \end{align*} $$
and the first matrix is invertible. By Lemma 4.1, both matrices appearing in the factorization above are commutators of a matrix in
![]() $\operatorname {\mathrm {GL}}_2(D)$
and a matrix in
$\operatorname {\mathrm {GL}}_2(D)$
and a matrix in
![]() $M_2(D)$
.
$M_2(D)$
.
Case 2: We have
![]() $s=0$
and
$s=0$
and
![]() $t \neq 0$
. Then,
$t \neq 0$
. Then,
 $$ \begin{align*} a = \begin{pmatrix} r & 0 \\ t & u \end{pmatrix} = \begin{pmatrix} 1 & -(u-r)t^{-1} \\ 0 & -1 \end{pmatrix} \begin{pmatrix} u & (u-r)t^{-1}u \\ -t & -u \end{pmatrix} \end{align*} $$
$$ \begin{align*} a = \begin{pmatrix} r & 0 \\ t & u \end{pmatrix} = \begin{pmatrix} 1 & -(u-r)t^{-1} \\ 0 & -1 \end{pmatrix} \begin{pmatrix} u & (u-r)t^{-1}u \\ -t & -u \end{pmatrix} \end{align*} $$
and the first matrix is invertible. Again by Lemma 4.1, both matrices are commutators of a matrix in
![]() $\operatorname {\mathrm {GL}}_2(D)$
and a matrix in
$\operatorname {\mathrm {GL}}_2(D)$
and a matrix in
![]() $M_2(D)$
.
$M_2(D)$
.
Case 3: We have
![]() $s \neq 0$
and
$s \neq 0$
and
![]() $t=0$
. This is analogous to case 2.
$t=0$
. This is analogous to case 2.
Case 4: We have
![]() $s=t=0$
. Then,
$s=t=0$
. Then,
 $$ \begin{align*} a = \begin{pmatrix} r & 0 \\ 0 & u \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & u \\ r & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} a = \begin{pmatrix} r & 0 \\ 0 & u \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & u \\ r & 0 \end{pmatrix} \end{align*} $$
and the first matrix is invertible. Once again by Lemma 4.1, both matrices are commutators of a matrix in
![]() $\operatorname {\mathrm {GL}}_2(D)$
and a matrix in
$\operatorname {\mathrm {GL}}_2(D)$
and a matrix in
![]() $M_2(D)$
.
$M_2(D)$
.
Lemma 4.3 Let D be a division ring containing at least three elements, let
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $1_n \in M_n(D)$
denote the identity matrix. Then, there exist
$1_n \in M_n(D)$
denote the identity matrix. Then, there exist
![]() $b,c,d,e \in M_n(D)$
such that
$b,c,d,e \in M_n(D)$
such that
![]() $1_n=[b,c][d,e]$
, and such that
$1_n=[b,c][d,e]$
, and such that
![]() $[b,c]$
and d are invertible.
$[b,c]$
and d are invertible.
Proof For
![]() $n=2$
this follows from Propostion 4.2, so we consider the case
$n=2$
this follows from Propostion 4.2, so we consider the case
![]() $n=3$
.
$n=3$
.
Since D contains at least three elements, we can choose
![]() $x\in D\setminus \{0,1\}$
. Then,
$x\in D\setminus \{0,1\}$
. Then,
![]() $y:=x-1$
is not zero. We have
$y:=x-1$
is not zero. We have
 $$ \begin{align*} \left[ \begin{pmatrix} 0 & 0 & -x \\ 1 & 0 & 0 \\ 0 & y & 0 \\ \end{pmatrix}, \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & -1 & 0 \end{pmatrix} \right] = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \left[ \begin{pmatrix} 0 & 0 & -x \\ 1 & 0 & 0 \\ 0 & y & 0 \\ \end{pmatrix}, \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & -1 & 0 \end{pmatrix} \right] = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} \end{align*} $$
and the matrix ![]() is invertible. Similarly, we see that
is invertible. Similarly, we see that ![]() is an (invertible) commutator in
is an (invertible) commutator in
![]() $M_3(D)$
. Since
$M_3(D)$
. Since ![]() , this establishes the case
, this establishes the case
![]() $n=3$
.
$n=3$
.
In preparation for the general case, let us fix matrices
![]() $b_2,c_2,d_2,e_2\in M_2(D)$
and
$b_2,c_2,d_2,e_2\in M_2(D)$
and
![]() $b_3,c_3,d_3,e_3\in M_3(D)$
satisfying
$b_3,c_3,d_3,e_3\in M_3(D)$
satisfying
and such that
![]() $\big [b_2,c_2\big ], \big [b_3,c_3\big ], d_2$
and
$\big [b_2,c_2\big ], \big [b_3,c_3\big ], d_2$
and
![]() $d_3$
are invertible. Given
$d_3$
are invertible. Given
![]() $n\geq 4$
, find
$n\geq 4$
, find
![]() $k,l\ge 0$
with
$k,l\ge 0$
with
![]() $n = 2k + 3l$
. Let
$n = 2k + 3l$
. Let
![]() $b\in M_n(D)$
be the block-diagonal matrix with k blocks
$b\in M_n(D)$
be the block-diagonal matrix with k blocks
![]() $b_2$
and l blocks
$b_2$
and l blocks
![]() $b_3$
. Define
$b_3$
. Define
![]() $c,d,e\in M_n(D)$
similarly. It is then easy to check that
$c,d,e\in M_n(D)$
similarly. It is then easy to check that
![]() $1_n=[b,c][d,e]$
, and that
$1_n=[b,c][d,e]$
, and that
![]() $[b,c]$
and d are invertible, thus finishing the proof.
$[b,c]$
and d are invertible, thus finishing the proof.
Theorem 4.4 Let D be a division ring with infinite center. Then every matrix in
![]() $M_n(D)$
for
$M_n(D)$
for
![]() $n \geq 2$
is a product of two commutators.
$n \geq 2$
is a product of two commutators.
Proof For every (not necessarily infinite) field F, every matrix in
![]() $M_n(F)$
for
$M_n(F)$
for
![]() $n \geq 2$
is a product of two commutators; see [Reference BothaBot97, Theorem 4.1]. Thus, we may assume that D is noncommutative.
$n \geq 2$
is a product of two commutators; see [Reference BothaBot97, Theorem 4.1]. Thus, we may assume that D is noncommutative.
We verify the following stronger result by induction over n: For all
![]() $a \in M_n(D)$
, there exist
$a \in M_n(D)$
, there exist
![]() $b,c,d,e \in M_n(D)$
such that
$b,c,d,e \in M_n(D)$
such that
![]() $a=[b,c][d,e]$
, and such that
$a=[b,c][d,e]$
, and such that
![]() $[b,c]$
and d are invertible.
$[b,c]$
and d are invertible.
The case
![]() $n=2$
follows from Propostion 4.2. Assume that the result holds for some
$n=2$
follows from Propostion 4.2. Assume that the result holds for some
![]() $n \geq 2$
, and let us verify it for
$n \geq 2$
, and let us verify it for
![]() $n+1$
.
$n+1$
.
Let
![]() $a \in M_{n+1}(D)$
. If a is central, then the result follows from Lemma 4.3. Thus, we may assume that a is noncentral. Then, by [Reference Amitsur and RowenAR94, Proposition 1.8], a is similar to a matrix whose
$a \in M_{n+1}(D)$
. If a is central, then the result follows from Lemma 4.3. Thus, we may assume that a is noncentral. Then, by [Reference Amitsur and RowenAR94, Proposition 1.8], a is similar to a matrix whose
![]() $(1,1)$
-entry is zero. (Note that the global assumption of [Reference Amitsur and RowenAR94] that division rings are finite-dimensional over their centers is not used in the proof of [Reference Amitsur and RowenAR94, Proposition 1.8].) Since the desired conclusion is invariant under similarity, we may assume, without loss of generality, that
$(1,1)$
-entry is zero. (Note that the global assumption of [Reference Amitsur and RowenAR94] that division rings are finite-dimensional over their centers is not used in the proof of [Reference Amitsur and RowenAR94, Proposition 1.8].) Since the desired conclusion is invariant under similarity, we may assume, without loss of generality, that
![]() $a_{11}=0$
. Let
$a_{11}=0$
. Let
![]() $b \in M_{1,n}(D)$
,
$b \in M_{1,n}(D)$
,
![]() $c \in M_{n,1}(D)$
and
$c \in M_{n,1}(D)$
and
![]() $x \in M_n(D)$
satisfy
$x \in M_n(D)$
satisfy
 $$\begin{align*}a = \begin{pmatrix} 0 & b \\ c & x \end{pmatrix}. \end{align*}$$
$$\begin{align*}a = \begin{pmatrix} 0 & b \\ c & x \end{pmatrix}. \end{align*}$$
Since D is noncommutative, there exist a nonzero commutator
![]() $d \in D$
. By the inductive assumption, we have
$d \in D$
. By the inductive assumption, we have
![]() $x=y[v,w]$
for an invertible commutator
$x=y[v,w]$
for an invertible commutator
![]() $y \in M_n(D)$
and
$y \in M_n(D)$
and
![]() $v \in \operatorname {\mathrm {GL}}_n(D)$
and
$v \in \operatorname {\mathrm {GL}}_n(D)$
and
![]() $w \in M_n(D)$
. Then,
$w \in M_n(D)$
. Then,
 $$\begin{align*}a = \begin{pmatrix} 0 & b \\ c & x \end{pmatrix} = \begin{pmatrix} d & 0 \\ 0 & y \end{pmatrix} \begin{pmatrix} 0 & d^{-1}b \\ y^{-1}c & [v,w] \end{pmatrix}. \end{align*}$$
$$\begin{align*}a = \begin{pmatrix} 0 & b \\ c & x \end{pmatrix} = \begin{pmatrix} d & 0 \\ 0 & y \end{pmatrix} \begin{pmatrix} 0 & d^{-1}b \\ y^{-1}c & [v,w] \end{pmatrix}. \end{align*}$$
The matrix ![]() is an invertible commutator in
is an invertible commutator in
![]() $M_{n+1}(D)$
. It remains to verify that
$M_{n+1}(D)$
. It remains to verify that ![]() is the commutator of some matrix in
is the commutator of some matrix in
![]() $\operatorname {\mathrm {GL}}_{n+1}(D)$
and a matrix in
$\operatorname {\mathrm {GL}}_{n+1}(D)$
and a matrix in
![]() $M_{n+1}(D)$
. For this, we will need a result of [Reference CohnCoh73], and we first recall some of its terminology.
$M_{n+1}(D)$
. For this, we will need a result of [Reference CohnCoh73], and we first recall some of its terminology.
An element
![]() $\lambda \in D$
is called a left eigenvalue of v if there exists a nonzero
$\lambda \in D$
is called a left eigenvalue of v if there exists a nonzero
![]() $\xi \in M_{n,1}(D)$
such that
$\xi \in M_{n,1}(D)$
such that
![]() $v\xi = \xi \lambda $
, and
$v\xi = \xi \lambda $
, and
![]() $\lambda $
is called a right eigenvalue if there exists a nonzero
$\lambda $
is called a right eigenvalue if there exists a nonzero
![]() $\eta \in M_{1,n}(D)$
such that
$\eta \in M_{1,n}(D)$
such that
![]() $\eta v = \lambda \eta $
. The set of all left and right eigenvalues is called the spectrum of v; see [Reference CohnCoh73]. By [Reference CohnCoh73, Proposition 2.5], an element
$\eta v = \lambda \eta $
. The set of all left and right eigenvalues is called the spectrum of v; see [Reference CohnCoh73]. By [Reference CohnCoh73, Proposition 2.5], an element
![]() $\lambda $
in the center
$\lambda $
in the center
![]() $Z(D)$
of D belongs to the spectrum of v if and only if
$Z(D)$
of D belongs to the spectrum of v if and only if
![]() $v-\lambda $
is singular (
$v-\lambda $
is singular (
![]() $\lambda $
is called a ‘singular eigenvalue’ of z). Further, by [Reference CohnCoh73, Theorem 2.4], the spectrum of v contains at most finitely many conjugacy classes. Consequently, there are at most finitely many
$\lambda $
is called a ‘singular eigenvalue’ of z). Further, by [Reference CohnCoh73, Theorem 2.4], the spectrum of v contains at most finitely many conjugacy classes. Consequently, there are at most finitely many
![]() $\lambda \in Z(D)$
such that
$\lambda \in Z(D)$
such that
![]() $v-\lambda $
is singular.
$v-\lambda $
is singular.
Using that
![]() $Z(D)$
is infinite, we obtain a nonzero
$Z(D)$
is infinite, we obtain a nonzero
![]() $\lambda \in Z(D)$
such that
$\lambda \in Z(D)$
such that
![]() $v-\lambda $
is invertible. We then have
$v-\lambda $
is invertible. We then have
 $$\begin{align*}\begin{pmatrix} 0 & d^{-1}b \\ y^{-1}c & [v,w] \end{pmatrix} = \left[ \begin{pmatrix} \lambda & 0 \\ 0 & v \end{pmatrix}, \begin{pmatrix} 0 & d^{-1}b(\lambda-v)^{-1} \\ (v-\lambda)^{-1}y^{-1}c & w \end{pmatrix} \right] \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0 & d^{-1}b \\ y^{-1}c & [v,w] \end{pmatrix} = \left[ \begin{pmatrix} \lambda & 0 \\ 0 & v \end{pmatrix}, \begin{pmatrix} 0 & d^{-1}b(\lambda-v)^{-1} \\ (v-\lambda)^{-1}y^{-1}c & w \end{pmatrix} \right] \end{align*}$$
and ![]() is invertible. This proves the inductive step and finishes the proof.
is invertible. This proves the inductive step and finishes the proof.
Recall that a division ring that is finite-dimensional over its center is called a central division algebra. Since every finite division ring is a field, Theorem 4.4 along with [Reference BothaBot97, Theorem 4.1] yields the following result.
Corollary 4.5 Let D be a central division algebra. Then, every matrix in
![]() $M_n(D)$
for
$M_n(D)$
for
![]() $n \geq 2$
is a product of two commutators.
$n \geq 2$
is a product of two commutators.
The comparison of Propostion 4.2 and Theorem 4.4 raises the following question:
Question 4.6 Can the assumption that D has infinite center be removed in Theorem 4.4?
For
![]() $n=2$
, the answer is “yes” by Propostion 4.2. The next proposition provides another such instance.
$n=2$
, the answer is “yes” by Propostion 4.2. The next proposition provides another such instance.
Proposition 4.7 Every singular matrix over a division ring is a product of two commutators.
Proof Let D be a division ring, let
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $a \in M_n(D)$
be non-invertible. By Propostion 4.2, we may assume that
$a \in M_n(D)$
be non-invertible. By Propostion 4.2, we may assume that
![]() $n \geq 3$
. We may also assume that D contains at least three elements, since otherwise D is a field and then every matrix over D is a product of two commutators by [Reference BothaBot97, Theorem 4.1].
$n \geq 3$
. We may also assume that D contains at least three elements, since otherwise D is a field and then every matrix over D is a product of two commutators by [Reference BothaBot97, Theorem 4.1].
Since D is a right K-Hermite ring and has Bass stable rank one by Example 3.12, we can apply Lemma 3.8 and deduce that a is similar to the product
![]() $bc$
for a lower triangular matrix b and an upper triangular matrix c with all diagonal entries equal to
$bc$
for a lower triangular matrix b and an upper triangular matrix c with all diagonal entries equal to
![]() $1$
. Since the statement is invariant under similarity, we may assume that
$1$
. Since the statement is invariant under similarity, we may assume that
![]() $a=bc$
. Further, since
$a=bc$
. Further, since
![]() $a=bc$
is not invertible, using that D is a division ring it follows that at least one of the diagonal entries of b is zero. Without loss of generality, upon taking a similar matrix we may assume that
$a=bc$
is not invertible, using that D is a division ring it follows that at least one of the diagonal entries of b is zero. Without loss of generality, upon taking a similar matrix we may assume that
![]() $b_{nn}=0$
.
$b_{nn}=0$
.
Using that D contains at least three elements and
![]() $n \geq 3$
, we can choose nonzero
$n \geq 3$
, we can choose nonzero
![]() $e_1,\ldots ,e_{n-1} \in D$
such that
$e_1,\ldots ,e_{n-1} \in D$
such that
![]() $e_1+\ldots +e_{n-1}=0$
. Let
$e_1+\ldots +e_{n-1}=0$
. Let
![]() $e \in M_n(D)$
be the diagonal matrix with diagonal entries
$e \in M_n(D)$
be the diagonal matrix with diagonal entries
![]() $e_1,\ldots ,e_{n-1},1$
. Then
$e_1,\ldots ,e_{n-1},1$
. Then
![]() $a=bc=(be^{-1})(ec)$
, and the matrix
$a=bc=(be^{-1})(ec)$
, and the matrix
![]() $be^{-1}$
is lower diagonal with diagonal entries
$be^{-1}$
is lower diagonal with diagonal entries
![]() $b_{1,1}e_1^{-1},\ldots ,b_{n-1,n-1}e_{n-1}^{-1}, b_{nn}$
. Similarly,
$b_{1,1}e_1^{-1},\ldots ,b_{n-1,n-1}e_{n-1}^{-1}, b_{nn}$
. Similarly,
![]() $ec$
is upper diagonal with diagonal entries
$ec$
is upper diagonal with diagonal entries
![]() $e_1,\ldots ,e_{n-1},1$
.
$e_1,\ldots ,e_{n-1},1$
.
Let
![]() $b'$
be equal to the matrix
$b'$
be equal to the matrix
![]() $be^{-1}$
, except with the
$be^{-1}$
, except with the
![]() $(n,n)$
-entry replaced by
$(n,n)$
-entry replaced by
![]() $-\sum _{j=1}^{n-1}b_{j,j}e_j^{-1}$
; and let
$-\sum _{j=1}^{n-1}b_{j,j}e_j^{-1}$
; and let
![]() $c'$
be equal to the matrix
$c'$
be equal to the matrix
![]() $ec$
, except with the
$ec$
, except with the
![]() $(n,n)$
-entry replaced by
$(n,n)$
-entry replaced by
![]() $0$
. Then
$0$
. Then
![]() $a=b'c'$
, and
$a=b'c'$
, and
![]() $b'$
and
$b'$
and
![]() $c'$
are triangular matrices with zero trace, therefore commutators by Theorem 3.5. The factorization is:
$c'$
are triangular matrices with zero trace, therefore commutators by Theorem 3.5. The factorization is:
 $$ \begin{align*} a &= \begin{pmatrix} b_{11} & 0 & 0 & \dots & 0 \\ b_{21} & b_{22} & 0 & & \vdots \\ \vdots & & \ddots \\ b_{n-1,1} & \ldots & & b_{n-1,n-1} & 0 \\ b_{n,1} & \ldots & & b_{n,n-1} & 0 \end{pmatrix} \begin{pmatrix} 1 & c_{1,2} & c_{1,3} & \dots & c_{1,n} \\ 0 & 1 & c_{2,3} & \dots & c_{2,n} \\ \vdots & & \ddots & & \vdots \\ 0 & \ldots & & 1 & c_{n-1,n} \\ 0 & \ldots & & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} b_{11}e_1^{-1} & 0 & 0 & \dots & 0 \\ \ast & b_{22}e_2^{-1} & 0 & & \vdots \\ \vdots & & \ddots \\ \ast & \ldots & & b_{n-1,n-1}e_{n-1}^{-1} & 0 \\ \ast & \ldots & & \ast & 0 \end{pmatrix} \begin{pmatrix} e_1 & \ast & \ast & \dots & \ast \\ 0 & e_2 & \ast & \dots & \ast \\ \vdots & & \ddots & & \vdots \\ 0 & \ldots & & e_{n-1} & \ast \\ 0 & \ldots & & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} b_{11}e_1^{-1} & 0 & \dots & 0 \\ \vdots & \ddots & & \vdots \\ \ast & \ldots & b_{n-1,n-1}e_{n-1}^{-1} & 0 \\ \ast & \ldots & \ast & -\sum_{j=1}^{n-1} b_{jj}e_j^{-1} \end{pmatrix} \begin{pmatrix} e_1 & \ast & \dots & \ast \\ \vdots & \ddots & & \vdots \\ 0 & \ldots & e_{n-1} & \ast \\ 0 & \ldots & 0 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} a &= \begin{pmatrix} b_{11} & 0 & 0 & \dots & 0 \\ b_{21} & b_{22} & 0 & & \vdots \\ \vdots & & \ddots \\ b_{n-1,1} & \ldots & & b_{n-1,n-1} & 0 \\ b_{n,1} & \ldots & & b_{n,n-1} & 0 \end{pmatrix} \begin{pmatrix} 1 & c_{1,2} & c_{1,3} & \dots & c_{1,n} \\ 0 & 1 & c_{2,3} & \dots & c_{2,n} \\ \vdots & & \ddots & & \vdots \\ 0 & \ldots & & 1 & c_{n-1,n} \\ 0 & \ldots & & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} b_{11}e_1^{-1} & 0 & 0 & \dots & 0 \\ \ast & b_{22}e_2^{-1} & 0 & & \vdots \\ \vdots & & \ddots \\ \ast & \ldots & & b_{n-1,n-1}e_{n-1}^{-1} & 0 \\ \ast & \ldots & & \ast & 0 \end{pmatrix} \begin{pmatrix} e_1 & \ast & \ast & \dots & \ast \\ 0 & e_2 & \ast & \dots & \ast \\ \vdots & & \ddots & & \vdots \\ 0 & \ldots & & e_{n-1} & \ast \\ 0 & \ldots & & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} b_{11}e_1^{-1} & 0 & \dots & 0 \\ \vdots & \ddots & & \vdots \\ \ast & \ldots & b_{n-1,n-1}e_{n-1}^{-1} & 0 \\ \ast & \ldots & \ast & -\sum_{j=1}^{n-1} b_{jj}e_j^{-1} \end{pmatrix} \begin{pmatrix} e_1 & \ast & \dots & \ast \\ \vdots & \ddots & & \vdots \\ 0 & \ldots & e_{n-1} & \ast \\ 0 & \ldots & 0 & 0 \end{pmatrix}. \end{align*} $$
5 Commutators with a fixed element
In this section, we consider the more general problem of presenting elements in matrix algebras by commutators with a fixed matrix a. This is obviously considerably more demanding than allowing arbitrary commutators, so we will restrict ourselves to matrices over a field F. Our goal is to prove Theorem D from the introduction.
We remark that, if a matrix
![]() $a\in M_n(F)$
has rank k, then any commutator
$a\in M_n(F)$
has rank k, then any commutator
![]() $[a,x]$
, with
$[a,x]$
, with
![]() $x\in M_n(F)$
, has rank at most
$x\in M_n(F)$
, has rank at most
![]() $2k$
. The same is therefore true for any product
$2k$
. The same is therefore true for any product
![]() $[a,x_1]\dots [a,x_m]$
, with
$[a,x_1]\dots [a,x_m]$
, with
![]() $x_i\in M_n(F)$
. In order to represent every matrix in
$x_i\in M_n(F)$
. In order to represent every matrix in
![]() $M_n(F)$
by commutators
$M_n(F)$
by commutators
![]() $[a,x]$
, their products are thus insufficient and we are forced to involve sums of products. Motivated by the invariant
$[a,x]$
, their products are thus insufficient and we are forced to involve sums of products. Motivated by the invariant
![]() $\xi $
from [Reference Gardella and ThielGT23, Definition 5.1] (see the introduction), we are particularly interested in sums of products of two commutators. Another motivation is the result by Mesyan [Reference MesyanMes06, Theorem 15] which states that every trace zero matrix can be written as a sum of two commutators with fixed matrices.
$\xi $
from [Reference Gardella and ThielGT23, Definition 5.1] (see the introduction), we are particularly interested in sums of products of two commutators. Another motivation is the result by Mesyan [Reference MesyanMes06, Theorem 15] which states that every trace zero matrix can be written as a sum of two commutators with fixed matrices.
Our approach is based on the concept of a derivation. Recall that a linear map D from an algebra A to itself is called a derivation if
![]() $D(xy)=D(x)y+ xD(y)$
for all
$D(xy)=D(x)y+ xD(y)$
for all
![]() $x,y\in A$
. For any
$x,y\in A$
. For any
![]() $a\in A$
, the map
$a\in A$
, the map
![]() $x\mapsto [a,x]$
is a derivation. Such derivations are called inner. The problem that we address can obviously be formulated in terms of inner derivations.
$x\mapsto [a,x]$
is a derivation. Such derivations are called inner. The problem that we address can obviously be formulated in terms of inner derivations.
Let us start with an observation which is implicit in Herstein’s paper [Reference HersteinHer78]. Let A be any algebra and let
![]() $D\colon A \to A$
be a derivation. A straightforward verification shows that for all
$D\colon A \to A$
be a derivation. A straightforward verification shows that for all
![]() $x,y,z\in A$
, we have
$x,y,z\in A$
, we have
Accordingly, if
![]() $D^3\ne 0$
, then the subalgebra
$D^3\ne 0$
, then the subalgebra
![]() $\overline {D(A)}$
generated by the image of D contains a nonzero ideal of A. In particular,
$\overline {D(A)}$
generated by the image of D contains a nonzero ideal of A. In particular,
![]() $\overline {D(A)}$
is equal to the whole algebra A if A is simple. More precisely, the above formula shows that every element in A is a sum of products of at most three elements from the image of D.
$\overline {D(A)}$
is equal to the whole algebra A if A is simple. More precisely, the above formula shows that every element in A is a sum of products of at most three elements from the image of D.
It should be remarked that the assumption that
![]() $D^3\ne 0$
is necessary. Indeed, every element
$D^3\ne 0$
is necessary. Indeed, every element
![]() $a\in A$
such that
$a\in A$
such that
![]() $a^2=0$
gives rise to the inner derivation
$a^2=0$
gives rise to the inner derivation
![]() $D(x)=[a,x]$
which, as can be easily checked, satisfies
$D(x)=[a,x]$
which, as can be easily checked, satisfies
![]() $D^3=0$
and
$D^3=0$
and
![]() $a\overline {D(A)} a=\{0\}$
. The latter implies that
$a\overline {D(A)} a=\{0\}$
. The latter implies that
![]() $\overline {D(A)}$
cannot be equal to A if
$\overline {D(A)}$
cannot be equal to A if
![]() $a\ne 0$
and A is simple.
$a\ne 0$
and A is simple.
The above observation, however, does not help us if we wish to present every element in A as a sum of products of exactly two elements from the image of an (inner) derivation D. A slightly more sophisticated approach is necessary to tackle this problem. We start with the following result.
Lemma 5.1 Let D be a derivation of an algebra A, and let
![]() $b,c\in A$
satisfy
$b,c\in A$
satisfy
![]() $D(b)c=0$
. Then,
$D(b)c=0$
. Then,
for all
![]() $x,z\in A$
. Therefore, if
$x,z\in A$
. Therefore, if
![]() $D(b)D(c)\ne 0$
and A is simple, then every element in A is a sum of elements of the form
$D(b)D(c)\ne 0$
and A is simple, then every element in A is a sum of elements of the form
![]() $D(x)D(y)$
with
$D(x)D(y)$
with
![]() $x,y\in A$
.
$x,y\in A$
.
Proof Note that
![]() $D(b)c =0$
implies
$D(b)c =0$
implies
and
from which the formula from the statement of the lemma follows. If
![]() $D(b)D(c)\ne 0$
, then this formula implies that the ideal of A generated by
$D(b)D(c)\ne 0$
, then this formula implies that the ideal of A generated by
![]() $D(b)D(c)$
is contained in the set of sums of elements of the form
$D(b)D(c)$
is contained in the set of sums of elements of the form
![]() $D(x)D(y)$
with
$D(x)D(y)$
with
![]() $x,y\in A$
. Therefore, this set is equal to A if A is simple.
$x,y\in A$
. Therefore, this set is equal to A if A is simple.
Lemma 5.1 raises the question of when do there exist elements
![]() $b,c\in A$
such that
$b,c\in A$
such that
![]() $D(b)c =0$
and
$D(b)c =0$
and
![]() $D(b)D(c)\ne 0$
. In light of our goal, we are interested in the case where D is an inner derivation and
$D(b)D(c)\ne 0$
. In light of our goal, we are interested in the case where D is an inner derivation and
![]() $A=M_n(F)$
. We will consider a somewhat more general situation in Lemma 5.3. To this end, we need a result of general interest which is almost certainly known. However, we were unable to find a reference that would cover vector spaces over arbitrary fields. We, therefore, provide a proof which was shown to us by Clément de Seguins Pazzis, who kindly allowed us to include it here.
$A=M_n(F)$
. We will consider a somewhat more general situation in Lemma 5.3. To this end, we need a result of general interest which is almost certainly known. However, we were unable to find a reference that would cover vector spaces over arbitrary fields. We, therefore, provide a proof which was shown to us by Clément de Seguins Pazzis, who kindly allowed us to include it here.
Recall that an endomorphism a of an F-vector space V is said to be algebraic if there exists a nonzero polynomial
![]() $p\in F[X]$
with coefficients in F such that
$p\in F[X]$
with coefficients in F such that
![]() $p(a)=0$
. Moreover, the degree of a is the smallest degree of such a polynomial.
$p(a)=0$
. Moreover, the degree of a is the smallest degree of such a polynomial.
Lemma 5.2 Let n be a natural number. An endomorphism a of a vector space V (over any field) is algebraic of degree at most n if and only if the set
![]() $\{v, av, \dots ,a^n v\}$
is linearly dependent for every
$\{v, av, \dots ,a^n v\}$
is linearly dependent for every
![]() $v\in V$
.
$v\in V$
.
Proof It suffices to prove the “if” part. Thus, assume that the set
![]() $\{v, av, \dots ,a^n v\}$
is linearly dependent for each
$\{v, av, \dots ,a^n v\}$
is linearly dependent for each
![]() $v\in V$
. Denote by
$v\in V$
. Denote by
![]() $V_v$
the linear span of this set, and by
$V_v$
the linear span of this set, and by
![]() $p_v$
the minimal polynomial of the restriction of a to
$p_v$
the minimal polynomial of the restriction of a to
![]() $V_v$
. Pick
$V_v$
. Pick
![]() $v_0\in V$
such that
$v_0\in V$
such that
![]() $p_{v_0}$
has maximal degree. Our goal is to show that
$p_{v_0}$
has maximal degree. Our goal is to show that
![]() $p_{v_0}(a) =0$
. Since the dimension of
$p_{v_0}(a) =0$
. Since the dimension of
![]() $V_{v_0}$
is at most n by our assumption, this will prove the result.
$V_{v_0}$
is at most n by our assumption, this will prove the result.
Fix
![]() $v\in V$
and let us show that
$v\in V$
and let us show that
![]() $p_{v_0}(a)v=0$
. Let
$p_{v_0}(a)v=0$
. Let
![]() $\tilde {a}$
denote the restriction of a to
$\tilde {a}$
denote the restriction of a to
![]() $V_{v_0}+ V_v$
, and let
$V_{v_0}+ V_v$
, and let
![]() $\tilde {p}$
be the minimal polynomial of
$\tilde {p}$
be the minimal polynomial of
![]() $\tilde {a}$
. Since
$\tilde {a}$
. Since
![]() $V_{v_0}\subseteq V_{v_0}+ V_v$
,
$V_{v_0}\subseteq V_{v_0}+ V_v$
,
![]() $p_{v_0}$
divides
$p_{v_0}$
divides
![]() $\tilde {p}$
. If
$\tilde {p}$
. If
![]() $\tilde {p}$
was equal to
$\tilde {p}$
was equal to
![]() $p_w$
for some
$p_w$
for some
![]() $w\in V$
, then it would follow, in view of the choice of
$w\in V$
, then it would follow, in view of the choice of
![]() $v_0$
, that
$v_0$
, that
![]() $p_{v_0}=\tilde {p}$
and hence
$p_{v_0}=\tilde {p}$
and hence
![]() $p_{v_0}(a)v=0$
, as desired.
$p_{v_0}(a)v=0$
, as desired.
The fact that
![]() $\tilde {p}$
is really equal to
$\tilde {p}$
is really equal to
![]() $p_w$
for some
$p_w$
for some
![]() $w\in V$
follows by examining the Frobenius canonical form of
$w\in V$
follows by examining the Frobenius canonical form of
![]() $\tilde {a}$
. Indeed,
$\tilde {a}$
. Indeed,
![]() $\tilde {a}$
can be represented in some basis as a block-diagonal matrix with blocks being companion matrices whose associated polynomials form a sequence that is nonincreasing with respect to the divisibility relation. The first polynomial in the sequence is the minimal polynomial
$\tilde {a}$
can be represented in some basis as a block-diagonal matrix with blocks being companion matrices whose associated polynomials form a sequence that is nonincreasing with respect to the divisibility relation. The first polynomial in the sequence is the minimal polynomial
![]() $\tilde {p}$
, and, denoting the degree of
$\tilde {p}$
, and, denoting the degree of
![]() $\tilde {p}$
by d, the first d vectors in the basis are
$\tilde {p}$
by d, the first d vectors in the basis are
![]() $w,aw,\dots , a^{d-1}w$
for some
$w,aw,\dots , a^{d-1}w$
for some
![]() $w\in \tilde {V}$
. Since these vectors are linearly independent, the degree of
$w\in \tilde {V}$
. Since these vectors are linearly independent, the degree of
![]() $p_w$
is at least d. On the other hand,
$p_w$
is at least d. On the other hand,
![]() $p_w$
divides
$p_w$
divides
![]() $\tilde {p}$
since
$\tilde {p}$
since
![]() $w\in \tilde {V}$
. Therefore,
$w\in \tilde {V}$
. Therefore,
![]() $\tilde {p}=p_w$
.
$\tilde {p}=p_w$
.
Lemma 5.3 Let
![]() $A $
be the algebra of all endomorphisms of the vector space V. Let
$A $
be the algebra of all endomorphisms of the vector space V. Let
![]() $a\in A$
and let D be the inner derivation given by
$a\in A$
and let D be the inner derivation given by
![]() $D(x) = [a,x]$
. If a is not algebraic of degree at most
$D(x) = [a,x]$
. If a is not algebraic of degree at most
![]() $2$
, then there exists an element
$2$
, then there exists an element
![]() $b \in A$
such that
$b \in A$
such that
![]() $D(b)b =0$
and
$D(b)b =0$
and
![]() $D(b)^2\ne 0$
.
$D(b)^2\ne 0$
.
Proof In light of our assumption, Lemma 5.2 shows that there exists
![]() $v\in V$
such that
$v\in V$
such that
![]() $a^2v$
does not lie in the linear span of
$a^2v$
does not lie in the linear span of
![]() $\{v, av\}$
. Therefore, there is a linear functional f on V such that
$\{v, av\}$
. Therefore, there is a linear functional f on V such that
![]() $f(v)= f(av)=0$
and
$f(v)= f(av)=0$
and
![]() $f(a^2v)=1$
. Let b be the rank one endomorphism defined by
$f(a^2v)=1$
. Let b be the rank one endomorphism defined by
![]() $bu= f(u)v$
for all
$bu= f(u)v$
for all
![]() $u\in V$
. Observe that
$u\in V$
. Observe that
![]() $b^2=bab=0$
and
$b^2=bab=0$
and
![]() $ba^2b=b$
. Consequently,
$ba^2b=b$
. Consequently,
![]() $D(b)b= ab^2 - bab=0$
and
$D(b)b= ab^2 - bab=0$
and
![]() $D(b)^2 = (ab - ba)^2 = -ba^2 b = -b\ne 0$
.
$D(b)^2 = (ab - ba)^2 = -ba^2 b = -b\ne 0$
.
We are now ready to prove the main result of the section. We note that the number of summands needed in statement (2) is at most
![]() $n^2$
, since this is the linear dimension of
$n^2$
, since this is the linear dimension of
![]() $M_n(F)$
. It is conceivable that the smallest number of summands needed may be related to the degree of the minimal polynomial of the matrix a, but we have not explored this any further.
$M_n(F)$
. It is conceivable that the smallest number of summands needed may be related to the degree of the minimal polynomial of the matrix a, but we have not explored this any further.
Theorem 5.4 Let F be a field, let
![]() $n\ge 2$
, and let
$n\ge 2$
, and let
![]() $a\in M_n(F)$
. The following two conditions are equivalent.
$a\in M_n(F)$
. The following two conditions are equivalent.
-
(1) The degree of the minimal polynomial of a is greater than
 $2$
.
$2$
. -
(2) Every element in
 $M_n(F)$
can be written as a sum of elements of the form
$M_n(F)$
can be written as a sum of elements of the form
 $[a,x][a,y]$
with
$[a,x][a,y]$
with
 $x,y\in M_n(F)$
.
$x,y\in M_n(F)$
.
Proof Let us show that (1) implies (2). Condition (1) can be read as saying that a is not algebraic of degree at most
![]() $2$
. If we denote by D the inner derivation given by
$2$
. If we denote by D the inner derivation given by
![]() $D(c)=[a,c]$
for
$D(c)=[a,c]$
for
![]() $c \in M_n(F)$
, then by Lemma 5.3 there exists an element
$c \in M_n(F)$
, then by Lemma 5.3 there exists an element
![]() $b\in A$
such that
$b\in A$
such that
![]() $D(b)b =0$
and
$D(b)b =0$
and
![]() $D(b)^2\ne 0$
.
$D(b)^2\ne 0$
.
Since
![]() $D(b)^2 \neq 0$
, and since the algebra
$D(b)^2 \neq 0$
, and since the algebra
![]() $M_n(F)$
is simple, we find a natural number M and elements
$M_n(F)$
is simple, we find a natural number M and elements
![]() $r_j,s_j \in M_n(F)$
for
$r_j,s_j \in M_n(F)$
for
![]() $j=1,\ldots ,M$
such that
$j=1,\ldots ,M$
such that
 $$\begin{align*}1 = \sum_{j=1}^M r_jD(b)^2s_j. \end{align*}$$
$$\begin{align*}1 = \sum_{j=1}^M r_jD(b)^2s_j. \end{align*}$$
Given
![]() $x \in M_n(F)$
, it follows from Lemma 5.1 that
$x \in M_n(F)$
, it follows from Lemma 5.1 that
 $$ \begin{align*} x &= \sum_{j=1}^M xr_jD(b)^2s_j = \sum_{j=1}^M \big( D(xr_jb)D(bs_j) - D(x)D(b^2s_j) \big) \\ &= \sum_{j=1}^M \big( [a,xr_jb][a,bs_j] + [a,x][a,-b^2s_j] \big). \end{align*} $$
$$ \begin{align*} x &= \sum_{j=1}^M xr_jD(b)^2s_j = \sum_{j=1}^M \big( D(xr_jb)D(bs_j) - D(x)D(b^2s_j) \big) \\ &= \sum_{j=1}^M \big( [a,xr_jb][a,bs_j] + [a,x][a,-b^2s_j] \big). \end{align*} $$
This proves (2).
In order to show the converse, assume that (1) does not hold and let us show that (2) does not hold either. The case where the degree of the minimal polynomial of a is
![]() $1$
is trivial, so we may assume that it is equal to
$1$
is trivial, so we may assume that it is equal to
![]() $2$
. Let
$2$
. Let
![]() $\bar {F}$
denote the algebraic closure of F and let
$\bar {F}$
denote the algebraic closure of F and let
![]() $\lambda ,\mu \in \bar {F}$
satisfy
$\lambda ,\mu \in \bar {F}$
satisfy
![]() $(a-\lambda 1_n)(a-\mu 1_n)=0$
. Using at the first step that
$(a-\lambda 1_n)(a-\mu 1_n)=0$
. Using at the first step that
![]() $\lambda 1_n$
and
$\lambda 1_n$
and
![]() $\mu 1_n$
commute with all the elements of
$\mu 1_n$
commute with all the elements of
![]() $M_n(F)$
, for all
$M_n(F)$
, for all
![]() $x,y\in M_n(F)$
we get
$x,y\in M_n(F)$
we get
 $$ \begin{align*} &[a,x][a,y] = [(a-\lambda 1_n),x][(a-\mu 1_n),y] \\ &\qquad = (a-\lambda 1_n)x(a-\mu 1_n)y - (a-\lambda 1_n)xy(a-\mu 1_n) + x(a-\lambda 1_n) y (a-\mu 1_n). \end{align*} $$
$$ \begin{align*} &[a,x][a,y] = [(a-\lambda 1_n),x][(a-\mu 1_n),y] \\ &\qquad = (a-\lambda 1_n)x(a-\mu 1_n)y - (a-\lambda 1_n)xy(a-\mu 1_n) + x(a-\lambda 1_n) y (a-\mu 1_n). \end{align*} $$
This implies that
Denoting by S the set of sums of elements of the form
![]() $[a,x][a,y]$
, we thus have
$[a,x][a,y]$
, we thus have
Assuming that
![]() $S= M_n(F)$
, it follows that
$S= M_n(F)$
, it follows that
![]() $(a-\mu 1_n)e_{ij} (a-\lambda 1_n)=0 $
for every matrix unit
$(a-\mu 1_n)e_{ij} (a-\lambda 1_n)=0 $
for every matrix unit
![]() $e_{ij}$
in
$e_{ij}$
in
![]() $M_n(F)$
, which in turn implies that
$M_n(F)$
, which in turn implies that
for every
![]() $z_{ij}\in \bar {F}$
. Thus, we deduce that
$z_{ij}\in \bar {F}$
. Thus, we deduce that
![]() $(a-\mu 1_n)M_n(\bar {F}) (a-\lambda 1_n)=\{0\}$
. However, this is impossible since
$(a-\mu 1_n)M_n(\bar {F}) (a-\lambda 1_n)=\{0\}$
. However, this is impossible since
![]() $a-\mu 1_n$
and
$a-\mu 1_n$
and
![]() $a-\lambda 1_n$
are nonzero matrices of
$a-\lambda 1_n$
are nonzero matrices of
![]() $M_n(\bar {F})$
. Therefore,
$M_n(\bar {F})$
. Therefore,
![]() $S\ne M_n(F)$
.
$S\ne M_n(F)$
.