Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-26T02:45:02.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Product of two involutions in quaternionic special linear group

Part of: Basic linear algebra Other groups of matrices Structure and classification of infinite or finite groups Special matrices

Published online by Cambridge University Press:  08 January 2025

Krishnendu Gongopadhyay Open the ORCID record for Krishnendu Gongopadhyay [Opens in a new window] ,
Tejbir Lohan Open the ORCID record for Tejbir Lohan [Opens in a new window]  and
Chandan Maity Open the ORCID record for Chandan Maity [Opens in a new window]
Krishnendu Gongopadhyay
Affiliation:
Indian Institute of Science Education and Research (IISER) Mohali, Knowledge City, Sector 81, S.A.S. Nagar 140306, Punjab, India e-mail: [email protected], [email protected]
Tejbir Lohan
Affiliation:
Indian Institute of Technology Kanpur, Kanpur 208016, Uttar Pradesh, India e-mail: [email protected] [email protected]
Chandan Maity*
Affiliation:
Indian Institute of Science Education and Research (IISER) Berhampur, Berhampur 760003, Odisha, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An element of a group is called reversible if it is conjugate to its own inverse. Reversible elements are closely related to strongly reversible elements, which can be expressed as a product of two involutions. In this paper, we classify the reversible and strongly reversible elements in the quaternionic special linear group $ \mathrm {SL}(n,\mathbb {H})$ and quaternionic projective linear group 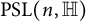$ \mathrm {PSL}(n,\mathbb {H})$. We prove that an element of 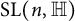$ \mathrm {SL}(n,\mathbb {H})$ (resp. 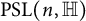$ \mathrm {PSL}(n,\mathbb {H})$) is reversible if and only if it is a product of two skew-involutions (resp. involutions).

Keywords

Reversible elementsstrongly reversible elementsquaternionic special linear groupWeyr canonical formreversing symmetry group

MSC classification

Primary: 20E45: Conjugacy classes 15B33: Matrices over special rings (quaternions, finite fields, etc.)
Secondary: 15A21: Canonical forms, reductions, classification 20H25: Other matrix groups over rings
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnol’d, V. I. and Avez, A., Ergodic problems of classical mechanics. Translated from the French by A. Avez, W. A. Benjamin, Inc., New York and Amsterdam, 1968, MR0232910.Google Scholar
Baake, M., A brief guide to reversing and extended symmetries of dynamical systems . In: Ergodic theory and dynamical systems in their interactions with arithmetics and combinatorics, Lecture Notes in Mathematics, 2213, pp. 117–135, MR3821715.CrossRefGoogle Scholar
Burton, D. M., Elementary number theory, 7th ed., McGraw-Hill, New York, 2011, ISBN: 978-0-07-338314-9.Google Scholar
Basmajian, A. and Maskit, B., Space form isometries as commutators and products of involutions . Trans. Amer. Math. Soc. 364(2012), no. 9, 5015–5033, MR2922617.CrossRefGoogle Scholar
Baake, M. and Roberts, J. A. G., The structure of reversing symmetry groups . Bull. Austral. Math. Soc. 73(2006), 445–459, MR2230652.CrossRefGoogle Scholar
Djoković, D. Ž., Product of two involutions . Arch. Math. (Basel) 18(1967), 582–584, MR0219550.CrossRefGoogle Scholar
Dutta, S., Gongopadhyay, K., and Lohan, T., Classification and decomposition of quaternionic projective transformations . Linear Algebra Appl. 676(2023), 66–87, MR4618023.CrossRefGoogle Scholar
Ellers, E. W., Products of two involutory matrices over skewfields . Linear Algebra Appl. 26(1979), 59–63, MR0535679.CrossRefGoogle Scholar
Gongopadhyay, K., Algebraic characterization of the isometries of the hyperbolic 5-space . Geom. Dedicata. 144(2010), 157–170, MR2580424.CrossRefGoogle Scholar
Gongopadhyay, K., Conjugacy classes in Möbius groups . Geom. Dedicata. 151(2011), 245–258, MR2780749.CrossRefGoogle Scholar
Gongopadhyay, K., Lohan, T., and Maity, C., Reversibility and real adjoint orbits of linear maps . In: Papadopoulos, A. (ed.), Essays in Geometry, dedicated to Norbert A’Campo, European Mathematical Society Press, Berlin, 2023, MR4631271.Google Scholar
Gongopadhyay, K., Lohan, T., and Maity, C., Product of two involutions in complex special linear group , preprint, 2023. arXiv:2307.07967.Google Scholar
Gongopadhyay, K., Lohan, T., and Maity, C., Reversibility of affine transformations . Proc. Edinb. Math. Soc. (2). 66(2023), no. 4, 1217–1228, MR4679222.CrossRefGoogle Scholar
Gongopadhyay, K. and Maity, C., Reality of unipotent elements in classical Lie groups. Bull. Sci. Math. 185(2023), Article no. 103261, MR4583694.CrossRefGoogle Scholar
Gill, N. and Singh, A., Real and strongly real classes in ${SL}_n(q)$ . J. Group Theory 14(2011), no. 3, 437–459, MR2794377.CrossRefGoogle Scholar
Hoffman, F. and Paige, E. C., Products of two involutions in the general linear group . Indiana Univ. Math. J. 20(1970/71), 1017–1020, MR0280508.CrossRefGoogle Scholar
Joven, J. P. E. and Paras, A. T., Agnes, products of skew-involutions . Electron. J. Linear Algebra 39(2023), 136–150, MR4573835.CrossRefGoogle Scholar
Lávička, R., O’Farrell, A., and Short, I., Reversible maps in the group of quaternionic Möbius transformations . Math. Proc. Cambridge Philos. Soc. 143(2007), no. 1, 57–69, MR2340975.CrossRefGoogle Scholar
Lamb, J. S. W. and Roberts, J. A. G., Time-reversal symmetry in dynamical systems: a survey . Phys. D. 112(1998), nos. 1–2, 1–39, MR1605826.CrossRefGoogle Scholar
O’Meara, K. C., Clark, J., Vinsonhaler, C. I., Advanced topics in linear algebra: Weaving matrix problems through the Weyr form, Oxford University Press, Oxford, 2011, MR2849857.Google Scholar
O’Farrell, A. G., Reversibility questions in groups arising in analysis . In: Complex analysis and potential theory, CRM Proceedings and Lecture Notes, 55, American Mathematical Society, Providence, RI, 2012, pp. 293–300, MR2986909.CrossRefGoogle Scholar
O’Farrell, A. G. and Short, I., Reversibility in Dynamics and Group Theory, Vol. 416. London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, 2015, MR3468569.CrossRefGoogle Scholar
Parker, J. R. and Short, I., Conjugacy classification of quaternionic Möbius transformations . Comput. Methods Funct. Theory. 9(2009), no. 1, 13–25, MR2478260.CrossRefGoogle Scholar
Paras, A. T. and Salinasan, J.R., The product of an involution and a skew-involution . Linear Algebra Appl. 584(2020), 431–437, MR4014740.CrossRefGoogle Scholar
Rodman, L.. Topics in quaternion linear algebra. Princeton Series in Applied Mathematics. Princeton University Press, Princeton, NJ, 2014, MR3241695.Google Scholar
Roche, A. and Vinroot, C. R., A factorization result for classical and similitude groups . Canad. Math. Bull. 61(2018), no. 1, 174–190, MR3746483.CrossRefGoogle Scholar
Shapiro, H., The Weyr Characteristic . Amer. Math. Monthly, 106, 1999, 919–929, MR1732500.CrossRefGoogle Scholar
Short, I., Reversible maps in isometry groups of spherical, Euclidean and hyperbolic space . Math. Proc. R. Ir. Acad. 108(2008), no. 1, 33–46, MR2448811.CrossRefGoogle Scholar
Singh, A. and Thakur, M., Reality properties of conjugacy classes in algebraic groups . Israel J. Math. 165(2008), 1–27, MR2403612.CrossRefGoogle Scholar
Tiep, P. H. and Zalesski, A. E., Real conjugacy classes in algebraic groups and finite groups of Lie type . J. Group Theory 8(2005), no. 3, 291–315, MR2137972.CrossRefGoogle Scholar
Wonenburger, M. J., Transformations which are products of two involutions . J. Math. Mech. 16(1966) 327–338, MR0206025.Google Scholar