Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T01:33:54.985Z Has data issue: false hasContentIssue false
  • English
  • Français

Probabilistic Proofs of the Little Riesz Theorem

Published online by Cambridge University Press:  20 November 2018

A. N. Al-Hussaini
A. N. Al-Hussaini*
Affiliation:
Department of Math. University of Alberta, Edmonton, Alberta T6G 2G1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following theorem is a widely used corollary of the Thorn-Riesz convexity theorem ([1], pp. 526).

Theorem. Let (Ω, a, μ) be a positive measure space, and let

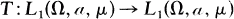
be a linear operator with ‖T‖1≤1, ‖T‖∞≤1. Then ‖T‖p≤1, 1≤p≤∞

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 4 , 01 December 1977 , pp. 443 - 445
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Dunford, N. and Schwartz, , Linear Operators, Part I, J. Wiley, 1958.Google Scholar
2. Hardy, G.H., Littlewood, J.E., and Polya, G., Inequalities. Cambridge University Press, 1952.Google Scholar
3. Lacey, H.E., The isometric theory of classical Banach spaces, Berlin, Springer-Verlag, 1974.Google Scholar
4. Rosenblatt, M., Markov processes; structure and asymptotic behavior, Berlin, Springer-Verlag, 1971.Google Scholar
5. Schaefer, H.H., Banach Lattices and Positive Operators. Springer-Verlag, 1974.Google Scholar