Article contents
Primitive Points in Rational Polygons
Published online by Cambridge University Press: 30 January 2020
Abstract
Let 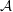 ${\mathcal{A}}$ be a star-shaped polygon in the plane, with rational vertices, containing the origin. The number of primitive lattice points in the dilate
${\mathcal{A}}$ be a star-shaped polygon in the plane, with rational vertices, containing the origin. The number of primitive lattice points in the dilate  $t{\mathcal{A}}$ is asymptotically
$t{\mathcal{A}}$ is asymptotically 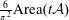 $\frac{6}{\unicode[STIX]{x1D70B}^{2}}\text{Area}(t{\mathcal{A}})$ as
$\frac{6}{\unicode[STIX]{x1D70B}^{2}}\text{Area}(t{\mathcal{A}})$ as 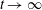 $t\rightarrow \infty$. We show that the error term is both
$t\rightarrow \infty$. We show that the error term is both 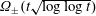 $\unicode[STIX]{x1D6FA}_{\pm }(t\sqrt{\log \log t})$ and
$\unicode[STIX]{x1D6FA}_{\pm }(t\sqrt{\log \log t})$ and 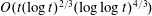 $O(t(\log t)^{2/3}(\log \log t)^{4/3})$. Both bounds extend (to the above class of polygons) known results for the isosceles right triangle, which appear in the literature as bounds for the error term in the summatory function for Euler’s
$O(t(\log t)^{2/3}(\log \log t)^{4/3})$. Both bounds extend (to the above class of polygons) known results for the isosceles right triangle, which appear in the literature as bounds for the error term in the summatory function for Euler’s 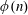 $\unicode[STIX]{x1D719}(n)$.
$\unicode[STIX]{x1D719}(n)$.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The first author was partially supported by ERC Advanced Research Grant no. 267165 (DISCONV) and by Hungarian National Science Grant K 111827. The second author was supported in part by a Natural Sciences and Engineering Research Council of Canada Discovery Grant. The fourth author was partially supported by ICERM, the Institute for Computational and Experimental Research in Mathematics, Brown University, and would like to thank the warm hospitality of the first author and the Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences.
References
- 1
- Cited by



