No CrossRef data available.
Article contents
A Practical Two-Dimensional Ergodic Theorem
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let τ:[0, 1] → [0, 1] be defined by τ(x) = 2x on [0, 1/2,] and τ(JC) = 2(1 - x) on [5, 1], and let T:[0, 1] x [0, 1] → [0, 1] x [0, 1] be defined by T(x,y) = (τ(x), τ(y))- Let
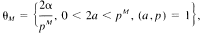
where p is a prime > 2, and a and M are integers. Consider T restricted to θM x θN, 1 < M < N. Let X = ((2a)/(pM), (2b)/(pN)) ∈ θM x θN and let per(X) denote the length of the period of X.
Then,
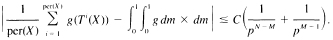
where m is Lebesque measure on [0, 1], and C is independent of p, N, M, a and b. Thus, as p → or as N - M and M→ →,
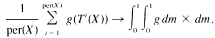
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1986
References
1.
Lasota, A. and Yorke, J. A., 0A? the existence of invariant measures for piecewise monotonie transformations, Trans. Amer. Math. Soc, 183 (1973), pp. 481–485.Google Scholar
2.
Scarowsky, M. and Boyarsky, A., Long periodic orbits of the triangle map, Proc. Amer. Math. Soc. (in press).Google Scholar
You have
Access