Article contents
Positive Solutions of the Falkner–Skan Equation Arising in the Boundary Layer Theory
Published online by Cambridge University Press: 20 November 2018
Abstract
The well-known Falkner–Skan equation is one of the most important equations in laminar boundary layer theory and is used to describe the steady two-dimensional flow of a slightly viscous incompressible fluid past wedge shaped bodies of angles related to 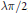 $\text{ }\!\!\lambda\!\!\text{ }\!\!\pi\!\!\text{ /2}$, where
$\text{ }\!\!\lambda\!\!\text{ }\!\!\pi\!\!\text{ /2}$, where 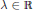 $\text{ }\!\!\lambda\!\!\text{ }\,\in \,\mathbb{R}$ is a parameter involved in the equation. It is known that there exists
$\text{ }\!\!\lambda\!\!\text{ }\,\in \,\mathbb{R}$ is a parameter involved in the equation. It is known that there exists
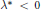 ${{\text{ }\!\!\lambda\!\!\text{ }}^{*}}\,<\,0$
such that the equation with suitable boundary conditions has at least one positive solution for each
${{\text{ }\!\!\lambda\!\!\text{ }}^{*}}\,<\,0$
such that the equation with suitable boundary conditions has at least one positive solution for each
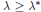 $\text{ }\!\!\lambda\!\!\text{ }\,\ge \,{{\text{ }\!\!\lambda\!\!\text{ }}^{*}}$
and has no positive solutions for
$\text{ }\!\!\lambda\!\!\text{ }\,\ge \,{{\text{ }\!\!\lambda\!\!\text{ }}^{*}}$
and has no positive solutions for
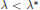 $\text{ }\!\!\lambda\!\!\text{ }\,<\,{{\text{ }\!\!\lambda\!\!\text{ }}^{*}}$
. The known numerical result shows
$\text{ }\!\!\lambda\!\!\text{ }\,<\,{{\text{ }\!\!\lambda\!\!\text{ }}^{*}}$
. The known numerical result shows
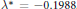 ${{\text{ }\!\!\lambda\!\!\text{ }}^{*}}\,=\,-0.1988$
. In this paper,
${{\text{ }\!\!\lambda\!\!\text{ }}^{*}}\,=\,-0.1988$
. In this paper,
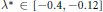 ${{\text{ }\!\!\lambda\!\!\text{ }}^{*}}\,\in \,[-0.4,\,-0.12]$
is proved analytically by establishing a singular integral equation which is equivalent to the Falkner–Skan equation. The equivalence result provides new techniques to study properties and existence of solutions of the Falkner–Skan equation.
${{\text{ }\!\!\lambda\!\!\text{ }}^{*}}\,\in \,[-0.4,\,-0.12]$
is proved analytically by establishing a singular integral equation which is equivalent to the Falkner–Skan equation. The equivalence result provides new techniques to study properties and existence of solutions of the Falkner–Skan equation.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2008
References
- 11
- Cited by


