Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T21:39:03.579Z Has data issue: false hasContentIssue false
  • English
  • Français

The Poset of Conjugacy Classes and Decomposition of Products in the Symmetric Group

Published online by Cambridge University Press:  20 November 2018

François Bédard  and
Alain Goupil
François Bédard
Affiliation:
Département de mathématiques et d'informatique, Université du Québec à Montréal, C.P. 8888 succ.A, Montréal, Québec H3C 3P8
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The action by multiplication of the class of transpositions of the symmetric group on the other conjugacy classes defines a graded poset 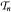as described by Birkhoff ([2]). In this paper, the edges of this poset are given a weight and the structure obtained is called the poset of conjugacy classes of the symmetric group. We use weights of chains in the posets 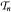to obtain new formulas for the decomposition of products of conjugacy classes of the symmetric group in its group algebra as linear combinations of conjugacy classes and we derive a new identity involving partitions of n.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 2 , 01 June 1992 , pp. 152 - 160
Copyright
Copyright © Canadian Mathematical Society 1992 

Footnotes

1

Partially supported by the FCAR (Québec)

References

1. Berge, C., Principes de combinatoire, Dunod, Paris, (1968).Google Scholar
2. Birkhoff, G., Lattice theory, (3rd ed.) Colloq. Publ. 25, Amer. Math. Soc, Providence R.I., (1967).Google Scholar
3. Burnside, W., Theory of groups of finite order, Second Edition, Dover, New York, (1955).Google Scholar
4. Denes, J., The Representation of a Permutation as the Product of a Minimal Number of Transpositions and its Connection to the Theory of Graphs, Publ. Math. Inst. Hungar. Acad. Sci. 4(1959), 63–70.Google Scholar
5. Farahat, H. K. and Higman, F. R. S., The Centres of Symmetric Group Rings, Proc. Roy. Soc. London, Series A 250(1950), 212–221.Google Scholar
6. Goupil, A., Produits de classes de conjugaison du groupe symétrique, Ph.D. Thesis, Université de Montréal, (1989).Google Scholar
7. Kreweras, G., Sur une classe de problèmes de dénombrement liés au treillis des partitions des entiers, Cahiers du bureau universitaire de recherche opérationelle, No. 6 Paris (1989).Google Scholar
8. Katriel, J. and Paldus, J. Explicit Expression for the Product of the Class of Transpositions with an arbitraryclass of the symmetric group, in Group Theoretical Methods in Physics, R. Gilmore, Editor, World Scientific Pub., Singapore, (1986).Google Scholar
9. Macdonald, I. G., Symmetric Functions and Hall Polynomials, Oxford University Press, New York, (1979).Google Scholar
10. Moon, J. W., Enumerating labelled trees. In: Graph Theory and Theoretical Physics, F. Harary, Academic Press, London and New York (1967), 261–271.Google Scholar
11. Stanley, R. P., Enumerative Combinatorics, Vol. I, Wadsworth and Brooks/Cole, Monterey, Cal., (1986).Google Scholar
12. Ziegler, G. M., On the Poset of Partitions of an Integer, Journal of Combinatorial Theory, Series A 42( 1986), 215–222.Google Scholar