Article contents
Polynomials for Kloosterman Sums
Published online by Cambridge University Press: 20 November 2018
Abstract
Fix an integer 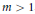 $m>1$, and set
$m>1$, and set 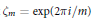 ${{\zeta }_{m}}=\exp \left( 2\pi i/m \right)$. Let
${{\zeta }_{m}}=\exp \left( 2\pi i/m \right)$. Let 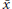 $\bar{x}$ denote the multiplicative inverse of
$\bar{x}$ denote the multiplicative inverse of 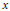 $x$ modulo
$x$ modulo 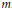 $m$. The Kloosterman sums
$m$. The Kloosterman sums 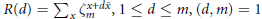 $R\left( d \right)=\sum\limits_{x}{\zeta _{m}^{x+d\bar{x}}},1\le d\le m,\left( d,m \right)=1$, satisfy the polynomial
$R\left( d \right)=\sum\limits_{x}{\zeta _{m}^{x+d\bar{x}}},1\le d\le m,\left( d,m \right)=1$, satisfy the polynomial
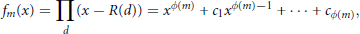 $${{f}_{m}}\left( x \right)=\underset{d}{\mathop{\prod }}\,\left( x-R\left( d \right) \right)={{x}^{\phi \left( m \right)}}+{{c}_{1}}{{x}^{\phi \left( m \right)-1}}+\cdot \cdot \cdot +{{c}_{\phi \left( m \right)}},$$
$${{f}_{m}}\left( x \right)=\underset{d}{\mathop{\prod }}\,\left( x-R\left( d \right) \right)={{x}^{\phi \left( m \right)}}+{{c}_{1}}{{x}^{\phi \left( m \right)-1}}+\cdot \cdot \cdot +{{c}_{\phi \left( m \right)}},$$
where the sum and product are taken over a complete system of reduced residues modulo 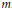 $m$. Here we give a natural factorization of
$m$. Here we give a natural factorization of 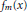 ${{f}_{m}}\left( x \right)$, namely,
${{f}_{m}}\left( x \right)$, namely,
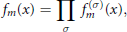 $${{f}_{m}}\left( x \right)=\underset{\sigma }{\mathop{\prod }}\,f_{m}^{\left( \sigma \right)}\left( x \right),$$
$${{f}_{m}}\left( x \right)=\underset{\sigma }{\mathop{\prod }}\,f_{m}^{\left( \sigma \right)}\left( x \right),$$
where 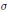 $\sigma$ runs through the square classes of the group
$\sigma$ runs through the square classes of the group 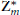 $Z_{m}^{*}$ of reduced residues modulo
$Z_{m}^{*}$ of reduced residues modulo 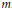 $m$. Questions concerning the explicit determination of the factors
$m$. Questions concerning the explicit determination of the factors 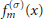 $f_{m}^{\left( \sigma \right)}\left( x \right)$ (or at least their beginning coefficients), their reducibility over the rational field
$f_{m}^{\left( \sigma \right)}\left( x \right)$ (or at least their beginning coefficients), their reducibility over the rational field 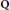 $\text{Q}$ and duplication among the factors are studied. The treatment is similar to what has been done for period polynomials for finite fields.
$\text{Q}$ and duplication among the factors are studied. The treatment is similar to what has been done for period polynomials for finite fields.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 2
- Cited by


