Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T13:16:31.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise Characterizations of Even Order Sobolev Spaces via Derivatives of Ball Averages

Part of: Linear function spaces and their duals Harmonic analysis in several variables

Published online by Cambridge University Press:  15 October 2018

Guangheng Xie ,
Dachun Yang  and
Wen Yuan
Guangheng Xie
Affiliation:
Laboratory of Mathematics and Complex Systems (Ministry of Education of China), School of Mathematical Sciences, Beijing Normal University, Beijing 100875, People’s Republic of China Email: [email protected]@[email protected]
Dachun Yang
Affiliation:
Laboratory of Mathematics and Complex Systems (Ministry of Education of China), School of Mathematical Sciences, Beijing Normal University, Beijing 100875, People’s Republic of China Email: [email protected]@[email protected]
Wen Yuan
Affiliation:
Laboratory of Mathematics and Complex Systems (Ministry of Education of China), School of Mathematical Sciences, Beijing Normal University, Beijing 100875, People’s Republic of China Email: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 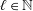$\ell \in \mathbb{N}$ and 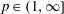$p\in (1,\infty ]$. In this article, the authors establish several equivalent characterizations of Sobolev spaces 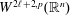$W^{2\ell +2,p}(\mathbb{R}^{n})$ in terms of derivatives of ball averages. The novelty in the results of this article is that these equivalent characterizations reveal some new connections between the smoothness indices of Sobolev spaces and the derivatives on the radius of ball averages and also that, to obtain the corresponding results for higher order Sobolev spaces, the authors first establish the combinatorial equality: for any 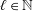$\ell \in \mathbb{N}$ and 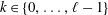$k\in \{0,\ldots ,\ell -1\}$, 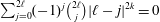$\sum _{j=0}^{2\ell }(-1)^{j}\binom{2\ell }{j}|\ell -j|^{2k}=0$.

Keywords

Sobolev spacepointwise characterizationball average

MSC classification

Primary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Secondary: 42B10: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type 42B25: Maximal functions, Littlewood-Paley theory 42B35: Function spaces arising in harmonic analysis
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 681 - 699
Copyright
© Canadian Mathematical Society 2019 

Footnotes

This project is supported by the National Natural Science Foundation of China (Grant Nos. 11571039, 11761131002, 11726621, 11671185 and 11871100). Dachun Yang is corresponding author.

References

Alabern, R., Mateu, J., and Verdera, J., A new characterization of Sobolev spaces on ℝ n . Math. Ann. 354(2012), 589–626. https://doi.org/10.1007/s00208-011-0738-0.Google Scholar
Belinsky, E., Dai, F., and Ditzian, Z., Multivariate approximating averages . J. Approx. Theory 125(2003), 85–105. https://doi.org/10.1016/j.jat.2003.09.005.Google Scholar
Chang, D.-C., Liu, J., Yang, D., and Yuan, W., Littlewood–Paley characterizations of Hajłasz–Sobolev and Triebel–Lizorkin spaces via averages on balls . Potential Anal. 46(2017), 227–259. https://doi.org/10.1007/s11118-016-9579-5.Google Scholar
Chang, D.-C., Yang, D., Yuan, W., and Zhang, J., Some recent developments of high order Sobolev-type spaces . J. Nonlinear Convex Anal. 17(2016), 1831–1865.Google Scholar
Coifman, R. R. and Weiss, G., Analyse Harmonique Non-commutative sur certains espaces homogènes. (French) Étude de Certaines Intégrales Singulières, Lecture Notes in Mathematics, 242, Springer-Verlag, Berlin–New York, 1971.Google Scholar
Coifman, R. R. and Weiss, G., Extensions of Hardy spaces and their use in analysis . Bull. Amer. Math. Soc. 83(1977), 569–645. https://doi.org/10.1090/S0002-9904-1977-14325-5.Google Scholar
Dai, F. and Ditzian, Z., Combinations of multivariate averages . J. Approx. Theory 131(2004), 268–283. https://doi.org/10.1016/j.jat.2004.10.003.Google Scholar
Dai, F., Gogatishvili, A., Yang, D., and Yuan, W., Characterizations of Sobolev spaces via averages on balls . Nonlinear Anal. 128(2015), 86–99. https://doi.org/10.1016/j.na.2015.07.024.Google Scholar
Dai, F., Gogatishvili, A., Yang, D., and Yuan, W., Characterizations of Besov and Triebel–Lizorkin spaces via averages on balls . J. Math. Anal. Appl. 433(2016), 1350–1368. https://doi.org/10.1016/j.jmaa.2015.08.054.Google Scholar
Dai, F., Liu, J., Yang, D., and Yuan, W., Littlewood–Paley characterizations of fractional Sobolev spaces via averages on balls . Proc. Roy. Soc. Edinburgh Sect. A. 148(2018), no. 6, 1135–1163. https://doi.org/10.1017/S0308 210517000440.Google Scholar
Hajłasz, P., Sobolev spaces on an arbitrary metric space . Potential Anal. 5(1996), 403–415. https://doi.org/10.1007/BF00275475.Google Scholar
Hajłasz, P. and Koskela, P., Sobolev met Poincaré . Mem. Amer. Math. Soc. 145(2000), no. 688, x+101pp. https://doi.org/10.1090/memo/0688.Google Scholar
He, Z., Yang, D., and Yuan, W., Littlewood–Paley characterizations of second-order Sobolev spaces via averages on balls . Canad. Math. Bull. 59(2016), 104–118. https://doi.org/10.4153/CMB-2015-038-9.Google Scholar
He, Z., Yang, D., and Yuan, W., Littlewood–Paley characterizations of higher-order Sobolev spaces via averages on balls . Math. Nachr. 291(2018), 284–325. https://doi.org/10.1002/mana.201600457.Google Scholar
Heinonen, J., Koskela, P., Shanmugalingam, N., and Tyson, J. T., Sobolev spaces on metric measure spaces, an approach based on upper gradients . New Mathematical Monographs, 27, Cambridge University Press, Cambridge, 2015. https://doi.org/10.1017/CBO9781316135914.Google Scholar
Hu, J., A note on Hajłasz–Sobolev spaces on fractals . J. Math. Anal. Appl. 280(2003), 91–101. https://doi.org/10.1016/S0022-247X(03)00039-8.Google Scholar
Rudin, W., Functional analysis . Second ed., International Series in Pure and Applied Mathematics. McGraw-Hill, Inc., New York, 1991.Google Scholar
Sato, S., Littlewood–Paley operators and Sobolev spaces . Illinois J. Math. 58(2014), 1025–1039.Google Scholar
Sato, S., Square functions related to integral of Marcinkiewicz and Sobolev spaces . Linear Nonlinear Anal. 2(2016), 237–252.Google Scholar
Sato, S., Littlewood–Paley equivalence and homogeneous Fourier multipliers . Integral Equations Operator Theory 87(2017), 15–44. https://doi.org/10.1007/s00020-016-2333-y.Google Scholar
Sato, S., Spherical square functions of Marcinkiewicz type with Riesz potentials . Arch. Math. (Basel) 108(2017), 415–426. https://doi.org/10.1007/s00013-017-1027-2.Google Scholar
Sato, S., Wang, F., Yang, D., and Yuan, W., Generalized Littlewood–Paley characterizations of fractional Sobolev spaces . Commun. Contemp. Math. 20(2018), no. 7, 1750077. https://doi.org/10.1142/S021919971750 0778.Google Scholar
Shanmugalingam, N., Newtonian spaces: an extension of Sobolev spaces to metric measure spaces . Rev. Mat. Iberoamericana 16(2000), 243–279. https://doi.org/10.4171/RMI/275.Google Scholar
Yang, D., New characterizations of Hajłasz–Sobolev spaces on metric spaces . Sci. China Ser. A 46(2003), 675–689. https://doi.org/10.1360/02ys0343.Google Scholar
Yang, D. and Yuan, W., Pointwise characterizations of Besov and Triebel–Lizorkin spaces in terms of averages on balls . Trans. Amer. Math. Soc. 369(2017), 7631–7655. https://doi.org/10.1090/tran/6871.Google Scholar
Yang, D., Yuan, W., and Zhou, Y., A new characterization of Triebel–Lizorkin spaces on ℝ n . Publ. Mat. 57(2013), 57–82. https://doi.org/10.5565/PUBLMAT_57113_02.Google Scholar
Zhang, Y., Chang, D.-C., and Yang, D., Generalized Littlewood–Paley characterizations of Triebel–Lizorkin spaces . J. Nonlinear Convex Anal. 18(2017), 1171–1190.Google Scholar
Zhang, J., Zhuo, C., Yang, D., and He, Z., Littlewood–Paley characterizations of Triebel–Lizorkin–Morrey spaces via ball averages . Nonlinear Anal. 150(2017), 76–103. https://doi.org/10.1016/j.na.2016.11.004.Google Scholar
Zhuo, C., Sickel, W., Yang, D., and Yuan, W., Characterizations of Besov-type and Triebel–Lizorkin-type spaces via averages on balls . Canad. Math. Bull. 60(2017), 655–672. https://doi.org/10.4153/CMB-2016-076-7.Google Scholar