Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T02:50:00.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Point Sets and Dynamical Systems In the Autocorrelation Topology

Published online by Cambridge University Press:  20 November 2018

Robert V. Moody  and
Nicolae Strungaru
Robert V. Moody
Affiliation:
Department of Mathematical and Statistical Sciences University of Alberta Edmonton, Alberta T6G 2G1
Nicolae Strungaru
Affiliation:
Department of Mathematical and Statistical Sciences University of Alberta Edmonton, Alberta T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

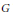This paper is about the topologies arising from statistical coincidence on locally finite point sets in locally compact Abelian groups $G$. The first part defines a uniform topology (autocorrelation topology) and proves that, in effect, the set of all locally finite subsets of 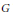$G$ is complete in this topology. Notions of statistical relative denseness, statistical uniform discreteness, and statistical Delone sets are introduced.

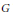The second part looks at the consequences of mixing the original and autocorrelation topologies, which together produce a new Abelian group, the autocorrelation group. In particular the relation between its compactness (which leads then to a $G$-dynamical system) and pure point diffractivity is considered. Finally for generic regular model sets it is shown that the autocorrelation group can be identified with the associated compact group of the cut and project scheme that defines it. For such a set the autocorrelation group, as a 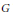$G$-dynamical system, is a factor of the dynamical local hull.

Keywords

52C2337B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 1 , 01 March 2004 , pp. 82 - 99
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Baake, M., Lenz, D., and Moody, R. V., Characterization of model sets by dynamical systems. In preparation.Google Scholar
[2] Baake, M. and Moody, R. V., Weighted Dirac combs with pure point diffraction. Journal für die reine und angewandteMathematik (Crelle's Journal), to appear.Google Scholar
[3] Bourbaki, N., Elements of Mathematics: General Topology. Chapters 1–4 and 5–10, Springer, Berlin, 1989, reprint.Google Scholar
[4] Meyer, Y., Algebraic Numbers and Harmonic Analysis. North-Holland, Amsterdam, 1972.Google Scholar
[5] Moody, R. V., Model sets: A survey. In: From Quasicrystals to More Complex Systems, (eds., F. Axel, F. Dénoyer and J. P. Gazeau), EDP Sciences, Les Ulis, and Springer, Berlin, 2000, 145–166.Google Scholar
[6] Moody, R. V., Uniform distribution in model sets. Canad. Math. Bull. 45(2002) 123–130.Google Scholar
[7] Radin, C. and Wolff, M., Space tilings and local isomorphism. Geom. Dedicata 42 (1992), 355–360.Google Scholar
[8] Rudin, W., Fourier Analysis on Groups. Wiley, New York, 1962; reprint, 1990.Google Scholar
[9] Schlottmann, M., Cut-and-project sets in locally compact Abelian groups. In: Quasicrystals and Discrete Geometry, (ed., J. Patera), Fields Inst. Monogr. 10, Amer. Math. Soc., Providence, RI, 1998, 247–264.Google Scholar
[10] Schlottmann, M., Generalized model sets and dynamical systems. In: Directions in Mathematical Quasicrystals, (eds., M. Baake and R. V. Moody), CRMMonograph Series 13, Amer.Math. Soc., Providence, RI, 2000, 143–159.Google Scholar