Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:25:43.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Plongements polyédraux tendus et nombre chromatique relatif des surfaces à bord

Part of: PL-topology Graph theory Low-dimensional topology Classical differential geometry Polytopes and polyhedra

Published online by Cambridge University Press:  28 December 2020

Pierre Jammes
Pierre Jammes*
Affiliation:
Université Côte d’Azur, CNRS, LJAD, France
*
e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Résumé

Le nombre chromatique relatif 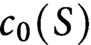$c_0(S)$ d’une surface compacte S à bord est défini comme la borne supérieure des nombres chromatiques des graphes plongés dans S avec tous leurs sommets sur 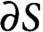$\partial S$ . Cet invariant topologique a été introduit pour l’étude de la multiplicité de la première valeur propre de Steklov sur S. Dans cet article, on montre que 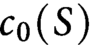$c_0(S)$ est aussi pertinent pour l’étude des plongements polyédraux tendus de S en établissant deux résultats. Le premier est que s’il existe un plongement polyédral tendu de S dans $\mathbb {R}^n$ qui n’est pas contenu dans un hyperplan, alors 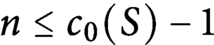$n\leq c_0(S)-1$ . Le second est que cette inégalité est optimale pour les surfaces de petit genre.

Keywords

Surfaces polyédralesnombre chromatiqueplongements tendus

MSC classification

Primary: 52B70: Polyhedral manifolds
Secondary: 57Q35: Embeddings and immersions 53A05: Surfaces in Euclidean space 57M15: Relations with graph theory 05C10: Planar graphs; geometric and topological aspects of graph theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 1001 - 1013
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banchoff, T. F., Tightly embedded $\ 2$ -dimensional polyhedral manifolds. Amer. J. Math. 87(1965), 462–472.CrossRefGoogle Scholar
Besson, G., Sur la multiplicité de la première valeur propre des surfaces riemanniennes. Ann. Inst. Fourier 30(1980), no. 1, 109–128.CrossRefGoogle Scholar
Cheng, S. Y., Eigenfunctions and nodal sets. Comment. Math. Helv. 51(1976), no. 1, 43–55.CrossRefGoogle Scholar
Colin de Verdière, Y., Construction de laplaciens dont une partie finie du spectre est donnée. Ann. scient. Éc. Norm. Sup. 20(1987), no. 4, 99–615.Google Scholar
Fraser, A. and Schoen, R., Eigenvalue bounds and minimal surfaces in the ball. Prépublication, 2012.Google Scholar
Grünbaum, B., On the facial structure of convex polytopes. Bull. Amer. Math. Soc. 71(1965), 559–560.Google Scholar
Heawood, P. J., Map-colour theorem. Quart. J. Pure Appl. Math. 24(1890), no. 96, p. 332–338.Google Scholar
Heffter, L., Ueber das Problem der Nachbargebiete. Math. Ann. 38(1891), no. 4, 477–508.CrossRefGoogle Scholar
Jammes, P., Prescription du spectre de Steklov dans une classe conforme. Anal. PDE 7(2014), no. 3, 529–550.CrossRefGoogle Scholar
Jammes, P., Multiplicité du spectre de Steklov sur les surfaces et nombre chromatique. Pacific J. Math. 282(2016), no. 1, 145–171.CrossRefGoogle Scholar
Karpukhin, M., Kokarev, G., and Polterovich, I., Multiplicity bounds for Steklov eigenvalues on Riemannian surfaces. Ann. Inst. Fourier 64(2014), no. 6, 2481–2502.CrossRefGoogle Scholar
Kühnel, W., Tight and $0$ -tight polyhedral embeddings of surfaces. Invent. Math. 58(1980), no. 2, 161–177.CrossRefGoogle Scholar
Kühnel, W., Tight polyhedral submanifolds and tight triangulations . Lect. Notes Math. 1612, Springer Verlag, Berlin, 1995.CrossRefGoogle Scholar
Möbius, A. F., Zur Theorie des Polyëder und der Elementarverwandschaft . In: Gesammelte Werke. Vol. 2. Hirzel, Leipzig, 1886, pp. 519–559.Google Scholar
Ringel, G., Map color theorem . Die Grundlehren der Mathematischen Wissenschaften, 209, Springer Verlag, New York-Heidelberg, 1974.CrossRefGoogle Scholar
Ringel, G. and Youngs, J. W. T., Solution of the Heawood map-coloring problem. Proc. Natl. Acad. Sci. USA 60(1968), 438–445.CrossRefGoogle ScholarPubMed
Sévennec, B., Multiplicité du spectre des surfaces: une approche topologique. Sémin. Théor. Spectr. Géom. 12(1994), 29–36.Google Scholar
Sévennec, B., Multiplicity of the second Schrödinger eigenvalue on closed surfaces. Math. Ann. 324(2002), no. 1, 195–211.Google Scholar