Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Antunović, Tonći
and
Veselić, Ivan
2008.
Sharpness of the Phase Transition and Exponential Decay of the Subcritical Cluster Size for Percolation on Quasi-Transitive Graphs.
Journal of Statistical Physics,
Vol. 130,
Issue. 5,
p.
983.
Lenz, Daniel
and
Veselić, Ivan
2009.
Hamiltonians on discrete structures: jumps of the integrated density of states and uniform convergence.
Mathematische Zeitschrift,
Vol. 263,
Issue. 4,
p.
813.
Lenz, Daniel
2009.
Continuity of Eigenfunctions of Uniquely Ergodic Dynamical Systems and Intensity of Bragg Peaks.
Communications in Mathematical Physics,
Vol. 287,
Issue. 1,
p.
225.
Müller, Peter
and
Stollmann, Peter
2011.
Random Walks, Boundaries and Spectra.
Vol. 64,
Issue. ,
p.
235.
Grimmett, Geoffrey R.
and
Manolescu, Ioan
2014.
Bond percolation on isoradial graphs: criticality and universality.
Probability Theory and Related Fields,
Vol. 159,
Issue. 1-2,
p.
273.
Germinet, François
Müller, Peter
and
Rojas-Molina, Constanza
2015.
Ergodicity and dynamical localization for Delone–Anderson operators.
Reviews in Mathematical Physics,
Vol. 27,
Issue. 09,
p.
1550020.
Coletti, Cristian F.
Miranda, Daniel
and
Mussini, Filipe
2016.
Invariance Under Quasi-isometries of Subcritical and Supercritical Behavior in the Boolean Model of Percolation.
Journal of Statistical Physics,
Vol. 162,
Issue. 3,
p.
685.
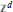 ${{\mathbb{Z}}^{d}}$, and to other percolation processes, including Bernoulli bond percolation.
${{\mathbb{Z}}^{d}}$, and to other percolation processes, including Bernoulli bond percolation.