Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T04:18:06.479Z Has data issue: false hasContentIssue false
  • English
  • Français

The Oscillatory Behavior of a First Order Non-Linear Differential Equation with Delay

Published online by Cambridge University Press:  20 November 2018

Forbes J. Burkowski  and
Peter J. Ponzo
Forbes J. Burkowski
Affiliation:
Department of Computer Science , University of Manitoba Winnipeg, Manitoba
Peter J. Ponzo
Affiliation:
Department of Computer Science , University of Manitoba Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Synopsis

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

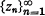This paper establishes the existence of an infinite set of zeros for the solution of a certain functional differential equation. The primary condition assuring this oscillatory behavior is expressed in terms of the magnitude of the delay.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 2 , 01 June 1974 , pp. 185 - 188
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Lillo, J. C., Oscillatory solutions of the equation y′(x)=m(x)y(x-n(x)), Journal of Differential Equations 6 (1969), 1-35.Google Scholar
2. Myshkis, A. D., Linear differential equations with retarded arguments, (German), Deutscher Verlag Der Wissenschaften, Berlin, 1955.Google Scholar
3. Feldstein, M. A. and Grafton, C. P., Retarded exponentials, Tech. Report AM28, Division of Applied Math., Brown University, May 1967.Google Scholar
4. Feldstein, M. A. and Graften, C. P., Experimental mathematics: An application to retarded differential equations with infinite lag, Proc. 1968 ACM National ConferenceGoogle Scholar
5. Ladas, G., Lakshmikantham, V. and Papadakis, J. S., Oscillations of higher-order retarded differential equations generated by the retarded argument, Tech. Report No. 20, Department of Mathematics, University of Rhode Island, January 1972.Google Scholar