Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-03T02:00:19.429Z Has data issue: false hasContentIssue false
  • English
  • Français

The Orthonormal Dilation Property for Abstract Parseval Wavelet Frames

Published online by Cambridge University Press:  20 November 2018

B. Currey  and
A. Mayeli
B. Currey
Affiliation:
Department of Mathematics and Computer Science, Saint Louis University, St. Louis, MO 63103, USA e-mail: [email protected]
A. Mayeli
Affiliation:
Mathematics Department, Queensborough College, City University of New York, 222-05 56th Avenue Bayside, NY 11364, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this work we introduce a class of discrete groups containing subgroups of abstract translations and dilations, respectively. A variety of wavelet systems can appear as 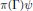$\pi \left( \Gamma \right)\psi $, where $\pi $ is a unitary representation of a wavelet group and $\Gamma $ is the abstract pseudo-lattice $\Gamma $. We prove a sufficent condition in order that a Parseval frame 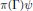$\pi \left( \Gamma \right)\psi $ can be dilated to an orthonormal basis of the form 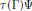$\tau \left( \Gamma \right)\Psi $, where $\tau $ is a super-representation of $\pi $. For a subclass of groups that includes the case where the translation subgroup is Heisenberg, we show that this condition always holds, and we cite familiar examples as applications.

Keywords

43A6542C4042C15frame, dilationwaveletBaumslag-Solitar groupshearlet
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 729 - 736
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Baggett, L., Furst, V., Merrill, K., and Packer, J. A., Generalized filters, the low-pass condition, and connections to multiresolution analysis. J. Funct. Anal. 257 (2009), no. 9, 2760–2779. http://dx.doi.org/10.1016/j.jfa.2009.05.004 Google Scholar
[2] Bownik, M., Jasper, J., and Speegle, D., Orthonormal dilations of non-tight frames. Proc. Amer. Math. Soc. 139 (2011), no. 9, 3247–3256. http://dx.doi.org/10.1090/S0002-9939-2011-10887-6 Google Scholar
[3] Currey, B. N., Decomposition and multiplicities for the quasiregular representation of algebraic solvable Lie groups. J. Lie Theory 19 (2009), no. 3, 557–612.Google Scholar
[4] Currey, B. and Mayeli, A., Gabor fields and wavelet sets for the Heisenberg group. Monatsh. Math. 162 (2011), no. 2, 119–142. http://dx.doi.org/10.1007/s00605-009-0159-2 Google Scholar
[5] Currey, B. and Mayeli, A., A density condition for interpolation on the Heisenberg group. Rocky Mountain J. Math. 42 (2012), no. 4, 1135–1151. http://dx.doi.org/10.1216/RMJ-2012-42-4-1135 Google Scholar
[6] Dahlke, S., Kutyniok, G., Steidl, G., and Teschke, G., Shearlet coorbit spaces and associated Banach frames. Appl. Comput. Harmon. Anal. 27 (2009), no. 2, 195–214. http://dx.doi.org/10.1016/j.acha.2009.02.004 Google Scholar
[7] Dutkay, D. E., Positive definite maps, representations, and frames Rev. Math. Phys. 16 (2004), no. 4, 451–477. http://dx.doi.org/10.1142/S0129055X04002047 Google Scholar
[8] Dutkay, D. E., Han, D., Picioraga, G., and Sun, Q., Orthonormal dilations of Parseval wavelets. Math. Ann. 341 (2008), no. 3, 483–515. http://dx.doi.org/10.1007/s00208-007-0196-x Google Scholar
[9] Easley, G., Labate, D., and Lim, W.-Q., Sparse directional image representations using the discrete shearlet transform. Appl. Comput. Harmon. Anal. 25 (2008), no. 1, 25–46. http://dx.doi.org/10.1016/j.acha.2007.09.003 Google Scholar
[10] Guo, K. and Labate, D., Optimally sparse multidimensional representation using shearlets. SIAM J. Math. Anal. 39 (2007), no. 1, 298–318. http://dx.doi.org/10.1137/060649781 Google Scholar
[11] Han, D. and Larsen, D., Frames, bases, and group representations. Mem. Amer. Math. Soc. 147 (2000), no. 697.Google Scholar