No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In this paper, it is proved that a reduced ring R has an orthogonal completion if and only if for every idempotent e e R, eR has an orthogonal completion. Every orthogonal subset X of R has a supremum in Q max(R), the maximal two sided ring of quotients of R, and the orthogonal completion of a reduced ring R, if it exists, is isomorphic to a unique subring of Q max(R). Hence the orthogonal completion of a reduced ring R, if it exists, is unique upto isomorphism. A reduced ring R has an orthogonal completion if and only if the collection of those elements of Q max(R) which are supremums of orthogonal subsets of R form a subring of Q max(R). Furthermore, every projectable ring R has an orthogonal completion 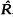 , which is a Baer ring. It is also proved that
, which is a Baer ring. It is also proved that 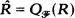 for projectable rings R, where
for projectable rings R, where 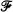 is the idempotent filter of those dense right ideals of R which contain a maximal orthogonal subset of idempotents of R.
is the idempotent filter of those dense right ideals of R which contain a maximal orthogonal subset of idempotents of R.