Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T16:09:13.654Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal Stopping Under General Dependence Conditions

Published online by Cambridge University Press:  20 November 2018

M. Longnecker
M. Longnecker*
Affiliation:
Texas A & M University, College Station, Texas 77843
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let {Xn} be a sequence of random variables, not necessarily independent or identically distributed, put 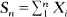and Mn =max0≤k≤n|Sk|. Effective bounds on 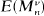in terms of assumed bounds on 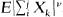, are used to identify conditions under which an extended-valued stopping time τ exists. That is these inequalities are used to guarantee the existence of the stopping time τ such that E(ST/aτ) = supt ∈ T∞ E(|Sτ|/at), where T∞ denotes the class of randomized extended-valued stopping times based on S1, S2, … and {an} is a sequence of constants. Specific applications to stochastic processes of the time series type are considered.

Keywords

60G4062L15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 3 , 01 September 1983 , pp. 260 - 266
Copyright
Copyright © Canadian Mathematical Society 1983

References

Basu, A. K. and Chow, Y. S. (1977). On the existence of optimal stopping rules for the reward sequence Sn/n. Sankhyā (Series A) 39, 278-289.Google Scholar
Davis, B. (1973). Moments of random walk having infinite variance and the existence of certain optimal stopping rules for Sn/n. Illinois J. Math. 17, 75-81.Google Scholar
Kenrick, G. W. (1929). The analysis of irregular motions with applications to the energyfrequency spectrum of static and of telegraph signals. Phil Mag. 7.Google Scholar
Klass, M. (1974). On stopping rules and the expected supremum of Sn/an and |Sn|/an. Ann. Prob. 2, 889-905.Google Scholar
Longnecker, M. and Serfling, R. J. (1975).On almost sure convergence of infinite series. Florida State University Statistics Report M346.Google Scholar
Longnecker, M. and Serfling, R. J. (1977). General moment and probability inequalities for the maximum partial sum. Acta Math. Acad. Sci. Hung. 30, 129-133.Google Scholar
Longnecker, M. and Serfling, R. J. (1978). Moment inequalities for Sn under general dependence restrictions, with applications. Z. Wahrscheinlichkeitstheorie 43, 1-21.Google Scholar
Magness, T. A., (1954). Spectral response of a quadratic device to non-Gaussian noise. /. Appl. Phys. 25, 1357–1365.Google Scholar
Siegmund, D. O. (1967). Some problems in the theory of optimal stopping rules. Ann. Math. Statist. 38, 1627-1640.Google Scholar
Wonham, W. M. and Fuller, A. T. (1958). Probability densities of the smoothed 'random telegraph signal. J. Electronics and Control 4, 567-576.Google Scholar