Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-13T08:45:11.475Z Has data issue: false hasContentIssue false
  • English
  • Français

On Valuations, Places and Graded Rings Associated to ∗-Orderings

Published online by Cambridge University Press:  20 November 2018

Igor Klep
Igor Klep*
Affiliation:
Institute for Mathematics, Physics and Mechanics, Department of Mathematics, University of Ljubljana, Jadranska 19, SI-1111 Ljubljana, Slovenia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study natural 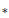$*$-valuations, 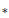$*$-places and graded 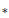$*$-rings associated with 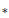$*$-ordered rings. We prove that the natural 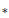$*$-valuation is always quasi-Ore and is even quasi-commutative (i.e., the corresponding graded 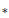$*$-ring is commutative), provided the ring contains an imaginary unit. Furthermore, it is proved that the graded 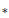$*$-ring is isomorphic to a twisted semigroup algebra. Our results are applied to answer a question of Cimprič regarding 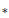$*$-orderability of quantum groups.

Keywords

14P1016S3016W10∗-orderingsvaluationsrings with involution
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 1 , 01 March 2007 , pp. 105 - 112
Copyright
Copyright © Canadian Mathematical Society 2007

References

[Ch] Chacron, M., c-orderable division rings with involution. J. Algebra 75(1982), no. 2, 495–522.Google Scholar
[Ci] Cimprič, J., Real spectra of quantum groups. J. Algebra 277(2004), no. 1, 282–297.Google Scholar
[CKM] Cimprič, J., Kochetov, M., and Marshall, M., Orderings and *-orderings on cocommutative Hopf algebras. To appear in Algebr. Represent. Theory, preprint available at http://vega.fmf.uni-lj.si/srag.Google Scholar
[Co] Cohn, P. M., On the embedding of rings in skew fields. Proc. London Math. Soc. 11(1961), 511–530.Google Scholar
[Cr] Craven, T., Places on *-fields and the real holomorphy ring. Comm. Algebra 18(1990), no. 9, 2791–2820.Google Scholar
[CS] Craven, T. and Smith, T., Ordered *-rings. J. Algebra 238(2001), no. 1, 314–327.Google Scholar
[Fu] Fuchs, L., Partially Ordered Algebraic Systems. Pergamon Press, Oxford, 1963.Google Scholar
[He] Herstein, I. N., Special simple rings with involution. J. Algebra 6(1967), no. 3, 369–375.Google Scholar
[Ho1] Holland, S. S., Orderings and square roots in *-fields. J. Algebra 46(1977), no. 1, 207–219.Google Scholar
[Ho2] Holland, S. S., Strong orderings of *-fields. J. Algebra 101(1986), no. 1, 16–46.Google Scholar
[KM] Klep, I. and Moravec, P., On *-orderable groups. J. Pure Appl. Algebra 200(2005), no. 1–2, 25–35.Google Scholar
[KKMZ] Kuhlmann, F.-V., Kuhlmann, S., Marshall, M., and Zekavat, M., Embedding ordered fields in formal power series fields. J. Pure Appl. Algebra 169(2002), no. 1, 71–90.Google Scholar
[Ma1] Marshall, M., *-orderings on a ring with involution. Comm. Algebra 28(2000), no. 3, 1157–1173.Google Scholar
[Ma2] Marshall, M., *-orderings and *-valuations on algebras of finite Gelfand-Kirillov dimension. J. Pure Appl. Algebra 179(2003), no. 3, 255–271.Google Scholar
[MZ1] Marshall, M., and Zhang, Y., Orderings, real places and valuations on noncommutative integral domains. J. Algebra 212(1999), no. 1, 190–207.Google Scholar
[MZ2] Marshall, M., and Zhang, Y., Orderings and valuations on twisted polynomial rings. Comm. Algebra 28(2000), no. 8, 3763–3776.Google Scholar