Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-08T21:33:48.321Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Uniqueness of Jordan Canonical Form Decompositions of Operators by K-theoretical Data

Published online by Cambridge University Press:  20 November 2018

Chunlan Jiang  and
Rui Shi
Chunlan Jiang
Affiliation:
Department of Mathematics, Hebei Normal University, Hebei, 050024, China e-mail: [email protected]
Rui Shi
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian, 116024, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we develop a generalized Jordan canonical form theorem for a certain class of operators in 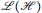$L\left( H \right)$ . A complete criterion for similarity for this class of operators in terms of 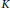$K$ -theory for Banach algebras is given.

Keywords

47A1547C1547A65strongly irreducible operatorsimilarity invariantreduction theory of von Neumann algebrasK-theory
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 326 - 339
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Azoff, E. A., Borel measurability in linear algebra. Proc. Amer. Math. Soc. 42(1974), 346–350. http://dx.doi.org/10.1090/S0002-9939-1974-0327799-1 Google Scholar
[2] Azoff, E. A., Fong, C. K., and Gilfeather, F., A reduction theory for non-self-adjoint operator algebras. Trans. Amer. Math. Soc. 224(1976), no. 2, 351–366. http://dx.doi.org/10.1090/S0002-9947-1976-0448109-1 Google Scholar
[3] Blackadar, B., K-theoryfor operator algebras.Second éd.,Mathematical Sciences Research Institute Publications, 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[4] Conway, J. B., A course in functional analysis. Second éd.,Graduate Texts in Mathematics, 96, Springer-Verlag, New York, 1990.Google Scholar
[5] Davidson, K. R.,C*-algebras by example. Fields Institute Monographs, 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
[6] Deckard, D. and Pearcy, C., On continuous matrix-valued functions on a Stonian space. Pacific J. Math. 14(1964), 857–869. http://dx.doi.org/10.2140/pjm.1964.14.857 Google Scholar
[7] Dowson, H. R., Spectral theory of linear operators.London Mathematical Society Monographs, 12, Academic Press, Inc., London-New York, 1978.Google Scholar
[8] Gilfeather, F., Strong reducibility of operators. Indiana Univ. Math. J. 22(1972), 393–397. http://dx.doi.org/10.1512/iumj.1973.22.22032 Google Scholar
[9] Halmos, P., Irreducible operators.Michigan Math. J. 15(1968), 215–223. http://dx.doi.org/10.1307/mmjV1028999975 Google Scholar
[10] Jiang, C. and Shi, R., Direct integrals of strongly irreducible operators.J. Ramanujan Math. Soc. 26(2011), no.,2 165–180.Google Scholar
[11] Jiang, C. and Wang, Z., Structure ofHilbert space operators. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2006.Google Scholar
[12] Radjavi, H. and Rosenthal, P., Invariant subspaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, 77, Springer-Verlag, New York-Heidelberg, 1973.Google Scholar
[13] Rordam, M., E Larsen, and Laustsen, N., An introduction to K-theoryfor C*-algebras. London Mathematical Society Student Texts, 49, Cambridge University Press, Cambridge, 2000.Google Scholar
[14] Schwartz, J. T., W*-algebras. Gordon and Breach, New York, 1967.Google Scholar
[15] Shi, R., On a generalization of the Jordan canonical form theorem on separable Hilbert spaces. Proc. Amer. Math. Soc. 140(2012), 1593–1604. http://dx.doi.org/10.1090/S0002-9939-2011-11513-2 Google Scholar
[16] Hou, Y. and Ji, K., On the extended holomorphic curves on C*-algebras. Oper. Matrices 8(2014), 999–1011. http://dx.doi.org/10.7153/oam-08-55 Google Scholar
[17] Ji, K., On a generalization ofBi(Cl) on C*-algebras. Proc. Indian Acad. Sci. Math. Sci. 124(2014), 243–253. http://dx.doi.org/!0.1007/s12044-014-0177-4 Google Scholar