Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T11:03:20.875Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Surjectivity of the Galois Representations Associated to Non-CM Elliptic Curves

Published online by Cambridge University Press:  20 November 2018

Alina Carmen Cojocaru  and
Ernst Kani
Alina Carmen Cojocaru
Affiliation:
The Fields Institute, 222 College Street, Toronto, ON, M5T 3J1 e-mail: [email protected]
Ernst Kani
Affiliation:
Queen's University, Department of Mathematics and Statistics, Kingston, ON, K7L 3N6 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

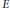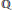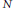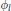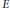Let $E$ be an elliptic curve defined over $\mathbb{Q}$, of conductor $N$ and without complex multiplication. For any positive integer $l$, let ${{\phi }_{1}}$ be the Galois representation associated to the $l$-division points of $E$. From a celebrated 1972 result of Serre we know that 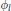${{\phi }_{1}}$ is surjective for any sufficiently large prime $l$. In this paper we find conditional and unconditional upper bounds in terms of 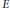$N$ for the primes $l$ for which 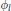${{\phi }_{1}}$ is not surjective.

Keywords

11G0511N3611R45
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 1 , 01 March 2005 , pp. 16 - 31
Copyright
Copyright © Canadian Mathematical Society 2005

References

[BCDT] Breuil, C., Conrad, B., Diamond, F. and Taylor, R., On the modularity of elliptic curves over ℚ: wild 3-adic exercises. J. Amer. Math. Soc. 14(2001), 843–939.Google Scholar
[Co] Cojocaru, A. C., Cyclicity of elliptic curves modulo p. PhD thesis, Queen's University, 2002.Google Scholar
[De] Deligne, P., Représentations l-adiques. Astérisque. 127(1985), 249–255.Google Scholar
[Hu] Huppert, B., Endliche Gruppen I. Grundlehren Math. Wiss., 134, Springer-Verlag, Berlin, 1967.Google Scholar
[Iw] Iwaniec, H., Topics in classical automorphic forms. Graduate Studies in Mathematics, 17, Amer. Math. Soc, Providence, RI, 1997.Google Scholar
[Kr] Kraus, A., Une remarque sur les points de torsion des courbes elliptiques. C. R. Acad. Sci. Paris, t. 321, Sér. I Math.321(1995), 1143–1146.Google Scholar
[La] Lang, S., Introduction to modular forms. Grundlehren Math. Wiss. 222, Springer-Verlag, Berlin, 1976.Google Scholar
[MaWü] Masser, D. W. and Wüstholz, G., Galois properties of division fields of elliptic curves. Bull. London Math. Soc. 25(1993), 247–254.Google Scholar
[Maz] Mazur, B., Rational isogenies of prime degree. Invent. Math. 44(1978), 129–162.Google Scholar
[Mer] Merel, Loic, Arithmetic of elliptic curves and diophantine equations. J. Théor. Nombres Bordeau. 11(1999), 173–200.Google Scholar
[RM97] RamMurty, M., Congruences between modular forms. In: Analytic Number Theory (ed. Motohashi, Y.), London Math. Soc. Lecture Note Series 247, 1997, pp. 309–320.Google Scholar
[RM99] RamMurty, M., Bounds for congruence primes. In: Automorphic Forms, Automorphic Representations and Arithmetic, (ed. Doran, Robert S., Dou, Ze-Li and Gilbert, George T.), Amer. Math. Soc., Providence, Ri, 1999, pp. 177–192.Google Scholar
[Se68] Serre, J.-P., Abelian l-adic representations and elliptic curves. W. A. Benjamin, New York, 1968.Google Scholar
[Se72] Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent.Math. 15(1972), 259–331.Google Scholar
[Se81] Serre, J.-P., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 123–201.Google Scholar
[Se85] Serre, J.-P., Collected papers. volume III, Springer-Verlag, 1985.Google Scholar
[Si84] Silverman, J. H., Heights and elliptic curves. In: Arithmetic Geometry (Cornell, G., Silverman, J. H., eds.), Springer-Verlag, New York, 1986, pp. 253–265.Google Scholar
[Si86] Silverman, J. H., The arithmetic of elliptic curves. Graduate Texts in Mathematics 106, Springer-Verlag, New York, 1986.Google Scholar
[StYu] Stewart, C. L. and Yu, Kunrui, On the ABC conjecture. Duke Math. J. 108(2001), 169–181.Google Scholar