Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T14:55:08.117Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Sum of Digits of Numerators of Bernoulli Numbers

Published online by Cambridge University Press:  20 November 2018

Attila Bérczes  and
Florian Luca
Attila Bérczes
Affiliation:
Institute of Mathematics, University of Debrecen, Number Theory Research Group, Hungarian Academy of Sciences e-mail: [email protected] University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary e-mail: [email protected]
Florian Luca
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autonoma de México, C.P. 58089, Morelia, Michoacán, México
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 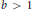$b\,>\,1$ be an integer. We prove that for almost all $n$, the sum of the digits in base $b$ of the numerator of the Bernoulli number 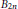${{B}_{2n}}$ exceeds $c$ log $n$, where 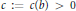$c\,:=\,c\left( b \right)\,>\,0$ is some constant depending on $b$.

Keywords

11B68Bernoulli numberssums of digits
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 723 - 728
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Erdős, P. and Wagstaff, S. S. Jr., The fractional parts of the Bernoulli numbers. Illinois J. Math. 24 (1980), no. 1, 104–112.Google Scholar
[2] Luca, F., The number of non-zero digits of n!. Canad. Math. Bull. 45 (2002), no. 1, 115–118. http://dx.doi.org/10.4153/CMB-2002-013-9 Google Scholar